Resorte con rozamiento seco
De Laplace
(→Enunciado) |
|||
| Línea 6: | Línea 6: | ||
# Al volver a comprimirse el muelle, la masa no retorna a su posición inicial. ¿A qué distancia de la pared se detiene instantáneamente? | # Al volver a comprimirse el muelle, la masa no retorna a su posición inicial. ¿A qué distancia de la pared se detiene instantáneamente? | ||
# ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada? | # ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada? | ||
| + | |||
| + | <center>[[Archivo:resorte-pared-rozamiento.png]]</center> | ||
==Máxima distancia sin rozamiento== | ==Máxima distancia sin rozamiento== | ||
| + | Cuando no hay rozamiento, el análisis es sencillo. | ||
| + | |||
| + | Tenemos un movimiento rectilíneo, por lo que podemos emplear cantidades escalares. | ||
| + | |||
| + | Si llamamos <math>x</math> a la distancia desde la pared, la ecuación de movimiento para la masa la da la ley de Hooke, | ||
| + | |||
| + | <center><math>ma = -k(x-l_0)\,</math></center> | ||
| + | |||
| + | La única fuerza que afecta al movimiento es la fuerza elástica debida al resorte. Además de esta actúan el peso y la reacción normal del plano, pero éstas se anulan mutuamente y no producen movimiento. | ||
| + | |||
| + | En la posición inicial el muelle está comprimido una cierta cantidad y a partir de ahí se suelta desde el reposo. El movimiento que describe la masa es un movimiento armónico simple alrededor de la posición de equilibrio | ||
| + | |||
| + | <center><math>x = l_0 + A\cos(\omega t-\varphi)\qquad\qquad \omega = \sqrt{\frac{k}{m}}</math></center> | ||
| + | |||
| + | Aplicando que conocemos la posición y la velocidad iniciales | ||
| + | |||
| + | <center><math>\left\{\begin{array}{rcl} x(t=0) & = & l_0-b = l_0+A\cos(\varphi) \\ v(t=0) & = & 0 =-A\omega\,\mathrm{sen}(-\varphi)\end{array}\right.\qquad\Rightarrow\qquad A=b\,\qquad\varphi = \pi</math></center> | ||
| + | |||
| + | De estas ecuaciones podría tomarse como solución que <math>A=-b</math>, <math>\varphi=0</math>, pero, aunque el resultado final es el mismo, debemos procurar tomar la amplitud como una cantidad positiva. Lo que nos dice la constante de fase <math>\varphi=\pi</math> es que la oscilación comienza en el punto de mínima elongación en lugar del de máxima. | ||
| + | |||
| + | La posición para todo instante es entonces de la forma | ||
| + | |||
| + | <center><math>x = l_0 + b\cos(\omega t - \pi) = l_0-b\cos(\omega t)</math></center> | ||
| + | |||
| + | |||
| + | |||
==Máxima distancia con rozamiento== | ==Máxima distancia con rozamiento== | ||
==Posición de la segunda parada== | ==Posición de la segunda parada== | ||
==Oscilaciones hasta la detención== | ==Oscilaciones hasta la detención== | ||
| - | + | ==Consideraciones sobre la energía== | |
| + | |||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 09:43 20 ene 2012
Contenido |
1 Enunciado
Se tiene una masa 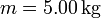 atada a un resorte de constante
atada a un resorte de constante  y longitud en reposo
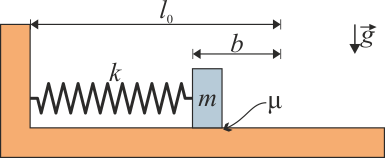
y longitud en reposo  . La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento μ = 0.10. El muelle se comprime una cantidad
. La masa reposa sobre una superficie horizontal sobre la que existe un pequeño coeficiente de rozamiento μ = 0.10. El muelle se comprime una cantidad 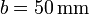 respecto a su posición de equilibrio.
respecto a su posición de equilibrio.
- Despreciando en primer lugar el rozamiento, determine la máxima distancia de la pared a la que llega la masa.
- Teniendo en cuenta el rozamiento, ¿cuánto vale la distancia de máximo alejamiento?
- Al volver a comprimirse el muelle, la masa no retorna a su posición inicial. ¿A qué distancia de la pared se detiene instantáneamente?
- ¿Al cabo de cuantas oscilaciones se detiene del todo? ¿Dónde se queda parada?
2 Máxima distancia sin rozamiento
Cuando no hay rozamiento, el análisis es sencillo.
Tenemos un movimiento rectilíneo, por lo que podemos emplear cantidades escalares.
Si llamamos x a la distancia desde la pared, la ecuación de movimiento para la masa la da la ley de Hooke,
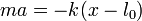
La única fuerza que afecta al movimiento es la fuerza elástica debida al resorte. Además de esta actúan el peso y la reacción normal del plano, pero éstas se anulan mutuamente y no producen movimiento.
En la posición inicial el muelle está comprimido una cierta cantidad y a partir de ahí se suelta desde el reposo. El movimiento que describe la masa es un movimiento armónico simple alrededor de la posición de equilibrio
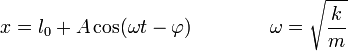
Aplicando que conocemos la posición y la velocidad iniciales
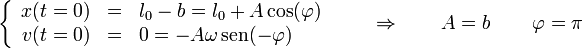
De estas ecuaciones podría tomarse como solución que A = − b, 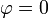 , pero, aunque el resultado final es el mismo, debemos procurar tomar la amplitud como una cantidad positiva. Lo que nos dice la constante de fase
, pero, aunque el resultado final es el mismo, debemos procurar tomar la amplitud como una cantidad positiva. Lo que nos dice la constante de fase 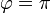 es que la oscilación comienza en el punto de mínima elongación en lugar del de máxima.
es que la oscilación comienza en el punto de mínima elongación en lugar del de máxima.
La posición para todo instante es entonces de la forma





