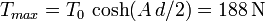Cable soportando su propio peso
De Laplace
(Página creada con '== Enunciado == right El cable en la figura tiene una densidad lineal de peso <math>w = 10.0\,\mathrm{N/m}</math>. La tensión en su punto m…') |
(→Solución) |
||
| Línea 34: | Línea 34: | ||
<math> | <math> | ||
T_{max} = T_0\,\cosh(A\,d/2) = 188\,\mathrm{N} | T_{max} = T_0\,\cosh(A\,d/2) = 188\,\mathrm{N} | ||
| - | |||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | [[Categoría: Problemas de armaduras y cables flexibles]] | ||
última version al 17:53 11 ene 2012
1 Enunciado
El cable en la figura tiene una densidad lineal de peso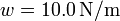 
. La tensión en su punto más bajo es 
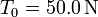. Calcula la distancia h y la tensión máxima en el cable.
2 Solución
La curva que describe la forma de un cable que sostiene únicamente su propio peso recibe el nombre de catenaria. Si el cable sólo tiene una fecha (los dos puntos de anclaje están a la misma altura) la función que describe la curva es
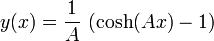
El origen de coordenadas se toma en el punto más bajo del cable. La constante A es el cociente entre el peso por unidad de longitud del cable y la tensión en el punto más bajo, T0. De los datos del enunciado
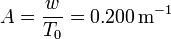
Para calcular la flecha usamos la expresión de la catenaria. Como los puntos de anclaje están a la misma altura, el punto más bajo del cable esta en el punto medio entre los dos anclajes. Es decir
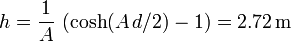
La tensión varía con la distancia al punto más bajo del cable
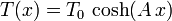
Es máxima en el punto más alejado del punto más bajo. En este caso, son los puntos de anclaje. La tensión máxima es
