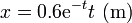Oscilador amortiguado
De Laplace
(→Rozamiento débil) |
(→Comparación de los tres casos) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 220: | Línea 220: | ||
====Comparación de los tres casos==== | ====Comparación de los tres casos==== | ||
[[Imagen:oamortiguadas.png|left]]Podemos comparar las tres soluciones. En las tres curvas tenemos la misma pendiente inicial, como corresponde a que la velocidad inicial en los tres casos sea la misma. El caso sobreamortiguado (o supercrítico) es el que antes se para (máximo de la curva) y a partir de ahí vuelve suavemente a la posición de equilibrio. El caso subamortiguado (o subcrítico) es el que llega más lejos y a partir de ahí vuelve y realiza oscilaciones (pasa por debajo de <math>x=0</math>) aunque muy atenuadas. En el caso crítico se para en una posición intermedia y luego vuelve a la posición de equilibrio rápidamente. Puede demostrarse¡ que el amortiguamiento crítico es la solución que menos tarda en quedarse en reposo (ni oscila, ni va demasiado despacio) y por tanto es la solución óptima a la hora de diseñar un amortiguador. | [[Imagen:oamortiguadas.png|left]]Podemos comparar las tres soluciones. En las tres curvas tenemos la misma pendiente inicial, como corresponde a que la velocidad inicial en los tres casos sea la misma. El caso sobreamortiguado (o supercrítico) es el que antes se para (máximo de la curva) y a partir de ahí vuelve suavemente a la posición de equilibrio. El caso subamortiguado (o subcrítico) es el que llega más lejos y a partir de ahí vuelve y realiza oscilaciones (pasa por debajo de <math>x=0</math>) aunque muy atenuadas. En el caso crítico se para en una posición intermedia y luego vuelve a la posición de equilibrio rápidamente. Puede demostrarse¡ que el amortiguamiento crítico es la solución que menos tarda en quedarse en reposo (ni oscila, ni va demasiado despacio) y por tanto es la solución óptima a la hora de diseñar un amortiguador. | ||
| + | |||
[[Categoría:Problemas de movimiento oscilatorio]] | [[Categoría:Problemas de movimiento oscilatorio]] | ||
| + | [[Categoría:Movimiento oscilatorio]] | ||
última version al 10:16 11 ene 2012
Contenido |
1 Enunciado
Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso 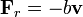 , de forma que su ecuación de movimiento, para un movimiento unidimensional es
, de forma que su ecuación de movimiento, para un movimiento unidimensional es
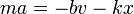
- Demuestre que la energía mecánica
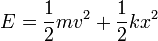
- Si buscamos una solución particular de la forma x = Aeλt, calcule los dos valores que puede tener λ. La solución general será una combinación de las dos posibilidades:
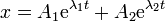
- ¿Cuál es el máximo valor de b para que haya oscilaciones? ¿cómo es el movimiento si b supera ese valor?
- Considere el caso particular de una partícula de masa
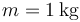 se encuentra sujeta a un muelle de constante
se encuentra sujeta a un muelle de constante
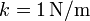 , existiendo un rozamiento b. Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad
, existiendo un rozamiento b. Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad 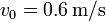 si (a)
si (a) 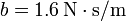 $; (b)
$; (b) 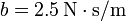 , (c)
, (c) 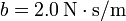 .
.
2 Solución
2.1 Disipación de la energía
Para ver que en presencia de rozamiento la energía mecánica se va perdiendo progresivamente, simplemente calculamos la derivada de la energía respecto al tiempo, para ver su signo.
Aplicando el mismo método que en el caso sin rozamiento
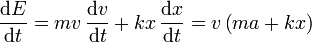
De acuerdo con al ecuación de movimiento para el oscilador armónico con rozamiento
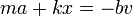
así que nos queda
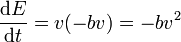
Esta cantidad siempre es negativa, por lo que la energía es una función que decrece de forma continuada. El decrecimiento no es constante. Se anula en los puntos de retorno (en los que la velocidad es cero) y es máximo cuando lo es la velocidad.
2.2 Soluciones exponenciales
Vamos a buscar ahora soluciones particulares de forma exponencial
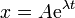
Calculamos la velocidad y la aceleración de este movimiento
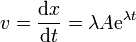
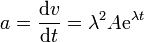
Sustituyendo en la ecuación de movimiento
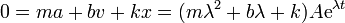
vemos que para que esta exponencial sea una solución, λ no puede tener cualquier valor, sino que debe cumplir la ecuación de segundo grado
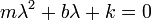
Resolviendo esta ecuación obtenemos dos posibles valores de λ
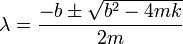
La solución general de la ecuación de movimiento será una combinación lineal de dos soluciones, una por cada exponente, exponenciales
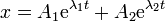
2.3 Oscilaciones amortiguadas
Dependiendo del valor de la constante de rozamiento b tenemos dos posibilidades para los valores de λ (en realidad, tres, pero la tercera la dejaremos por ahora).
2.3.1 Rozamiento fuerte
Cuando b es lo suficientemente grande
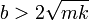

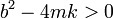
esto quiere decir que la raíz que aparece en la expresión del exponente λ es real. Por tanto, los dos valores de λ son reales y negativos (uno más grande en magnitud que el otro). La solución general es una combinación de dos exponenciales decrecientes
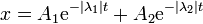
en este caso no hay oscilación alguna, sino que la partícula tiende, de forma más o menos rápida, hacia la posición de equilibrio x = 0.
Este caso de conoce como de oscilador sobreamortiguado o amortiguamiento supercrítico.
2.3.2 Rozamiento débil
Si el coeficiente b es lo suficientemente pequeño
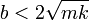

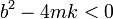
Tenemos entonces que en la expresión de λ aparece la raíz de número negativo, que es una cantidad imaginaria. De hecho, resultan dos valores para el exponente que son complejos conjugados
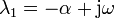
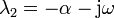
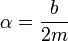
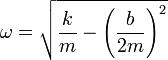
Una exponencial de un número imaginario significa una oscilación, ya que, por aplicación de la fórmula de Euler tenemos que
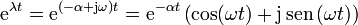
de forma que la solución general de la ecuación de movimiento se puede escribir en la forma
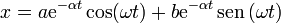
Cada una de estos sumandos es lo que se conoce como oscilaciones amortiguadas: la elongación varía con el tiempo como un coseno o un seno, pero la amplitud de esas oscilaciones decae exponencialmente. Al final, pasado un tiempo más o menos largo dependiendo de la intensidad del rozamiento, la partícula tiende a la posición de equilibrio x = 0.
Este caso de conoce como de oscilador subamortiguado o amortiguamiento subcrítico.
Así pues, el valor máximo para que haya oscilaciones es
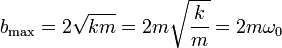
con ω0 la frecuencia que tendría el oscilador si no hubiera rozamiento.
2.4 Casos particulares
En este apartado se trata de hallar la solución completa para tres situaciones que parten de la misma condición inicial, pero con diferentes coeficientes de rozamiento. No nos basta con calcular los exponentes λ1 y λ2, sino que además debemos halalr las constantes A1 y A2.
calculemos en primer lugar los valores de los exponentes. Emplearemos en todos los cálculos el sistema internacional. Tenemos que para los tres casos, la frecuencia propia
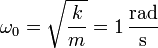
Los exponentes cumplen en los tres casos
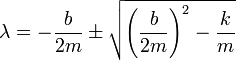
y esto nos da, en cada caso
2.4.1 Si b = 1.6 N·s/m (subamortiguado)
Sustituyendo en la ecuación de los exponentes
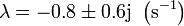
Los exponentes son complejos conjugados, por lo que el sistema posee amortiguamiento subcrítico y las soluciones son oscilaciones amortiguadas, que podemos escribir como
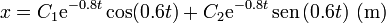
Imponiendo las condiciones iniciales tenemos que
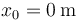
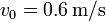
Del primer valor

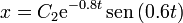
Derivando aquí obtenemos la velocidad
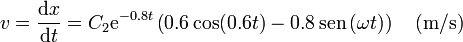
Imponiendo la condición inicial
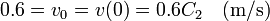

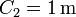
Por tanto, la solución completa para este caso es
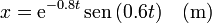
2.4.2 Si b = 2.5 N·s/m (sobreamortiguado)
Sustituyendo
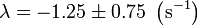

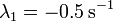
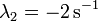
Los exponentes son ambos reales y negativos, por lo que el sistema posee amortiguamiento supercrítico y las soluciones son combinaciones de exponenciales decrecientes
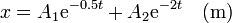
Imponiendo las condiciones iniciales tenemos que
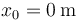
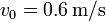
Del primer valor
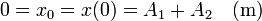
Derivando obtenemos la velocidad
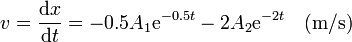
Imponiendo la condición inicial
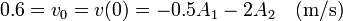
Nos queda el sistema de dos ecuaciones con dos incógnitas
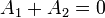
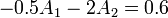
con solución
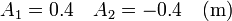
Así que la solución para este caso es
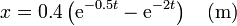
2.4.3 Si b = 2.0 N·s/m (crítico)
El caso b = 2.0 N·s/m es especial, ya que
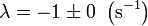

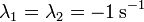
Si los dos exponentes son iguales, ¿cómo podemos escribir la solución como una combinación de dos exponenciales?
Para evitar entrar en toda la teoría de ecuaciones diferenciales, vamos a resolver este caso considerándolo como un caso límite.
Supongamos que b < 2 y luego tomaremos el límite  . Para un valor de b subcrítico, los exponentes valen
(sutituyendo m y k)
. Para un valor de b subcrítico, los exponentes valen
(sutituyendo m y k)
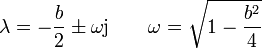
y la solución puede escribirse como
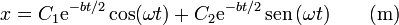
Imponiendo las condiciones iniciales resulta
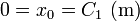
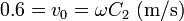
así que la solución para todo b subcrítico es
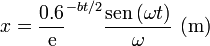
Consideremos el límite 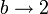 . En este límite
. En este límite
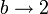
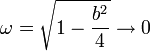
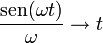
y por tanto la solución en este caso es