Deslizamiento entre dos rodillos
De Laplace
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
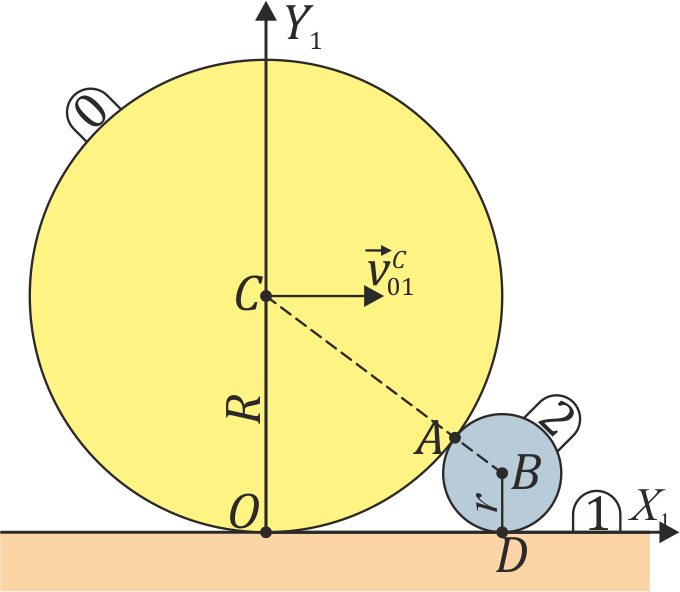
Un rodillo de radio <math>R=60\,\mathrm{cm}</math> (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro <math>C</math> avanza con una celeridad constante <math>v_0=30\,\mathrm{cm}/\mathrm{s}</math> respecto al suelo. En su | Un rodillo de radio <math>R=60\,\mathrm{cm}</math> (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro <math>C</math> avanza con una celeridad constante <math>v_0=30\,\mathrm{cm}/\mathrm{s}</math> respecto al suelo. En su | ||
marcha, este rodillo empuja a un segundo rodillo de radio <math>r=15\,\mathrm{cm}</math> (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura). | marcha, este rodillo empuja a un segundo rodillo de radio <math>r=15\,\mathrm{cm}</math> (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura). | ||
Revisión de 21:47 10 ene 2012
Contenido |
1 Enunciado
Un rodillo de radio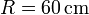 
(sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante 
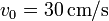respecto al suelo. En su
marcha, este rodillo empuja a un segundo rodillo de radio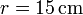 
(sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos. ¿Cuál es la rapidez de este deslizamiento?
2 Introducción
El deslizamiento entre los dos rodillos se debe a que ambos ruedan sobre el suelo, con lo que necesariamente la velocidad del punto A de un rodillo y la del punto A correspondiente del segundo será diferente, de forma que uno de los rodillos resbala sobre el otro.
La velocidad de deslizamiento será la diferencia de las velocidades respectivas
donde con el subíndice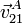 
se indica la velocidad de un punto A del rodillo pequeño “2” respecto a “1” (el suelo). Del mismo modo con 
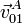se indica la velocidad del mismo punto como parte del rodillo grande “0” respecto al suelo “1”.
Calcularemos por separado estas dos velocidades y posteriormente hallaremos su diferencia. Si los cálculos son correctos debe resultarnos una velocidad tangente a la superficie de contacto.
