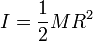Cálculo de momentos de inercia
De Laplace
(→Corona cilíndrica) |
(→Corona cilíndrica) |
||
| Línea 43: | Línea 43: | ||
mientras que la distancia al eje de los puntos de cada capa es <math>r</math>. Esto nos da la integral para el momento de inercia | mientras que la distancia al eje de los puntos de cada capa es <math>r</math>. Esto nos da la integral para el momento de inercia | ||
| - | <center><math>I = \frac{M}{V}\int_{R_1}^{R_2} r^2(2\pi r H)\,\mathrm{d}r=\frac{M}{V}\left(2\pi H\right | + | <center><math>I = \frac{M}{V}\int_{R_1}^{R_2} r^2(2\pi r H)\,\mathrm{d}r=\frac{M}{V}\left(2\pi H\right)\left(\frac{R_2^4}{4}-\frac{R_1^4}{4}\right) = \frac{M \pi H (R_2^4-R_1^4)}{2V}</math></center> |
El volumen total de esta corona es | El volumen total de esta corona es | ||
Revisión de 14:19 6 ene 2012
Contenido |
1 Enunciado
Halle los siguientes momentos de inercia de sólidos de densidad homogénea:
- Una corona cilíndrica de masa M radio interior R1 y exterior R2, con altura h, respecto al eje del cilindro.
- Una corona esférica de masa M, radio interior R1 y exterior R2, con respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado en el caso de una esfera maciza y de una superficie esférica?
- Una placa cuadrada de masa M y lado b respecto a:
- Un eje perpendicular a ella y que pasa por el centro.
- Un eje que pasa por dos vértices opuestos.
- Un eje que pasa por los centros de dos lados opuestos.
- Un paralelepípedo de masa M y lados a, b y c, respecto a un eje que pasa por los centros de dos caras opuestas.
- Un péndulo compuesto formado por una barra de longitud H y masa M1 y un disco de radio R y masa M2 clavado en un extremo de la barra respecto a un eje perpendicular al plano del disco y que pasa por el otro extremo de la barra.
2 Introducción
El momento de inercia de un sólido respecto a un eje se define como la cantidad
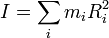
donde Ri es la distancia de la masa mi respecto al eje en cuestión. En el caso de una distribución continua, la suma se transforma en la integral correspondiente
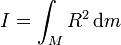
En el caso particular de que tomemos como eje Z el que usamos para hallar el momento de inercia, esta integral se expresa
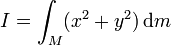
Si se sabe que los sólidos son homogéneos, quiere decir que su densidad de masa es la misma en todos sus puntos
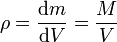
y por tanto, la masa de cada elemento es proporcional al volumen que ocupa
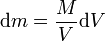
El cálculo del momento de inercia se convierte entonces en el de una integral de volumen (o de superficie para una figura plana)
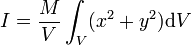
Sin embargo, el objeto de este problema no es calcular una ristra de integrales dobles o triples. La mayoría de estos momentos de inercia (que son los que aparecen más frecuentemente en problemas diversos) se pueden simplificar notablemente aprovechando las simetrías de la figura, que reducen el cálculo como mucho a una integral de una variable.
3 Corona cilíndrica
Dividimos la corona cilíndrica en finas capas concéntricas, de radio r y espesor dr. El volumen diferencial de cada una de estas capas es
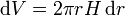
mientras que la distancia al eje de los puntos de cada capa es r. Esto nos da la integral para el momento de inercia
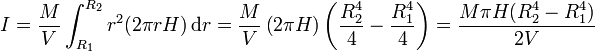
El volumen total de esta corona es
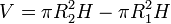
lo que nos da el momento de inercial
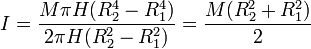
Como caso particular de este resultado tenemos:
- Superficie cilíndrica
- Tiene R1 = R2 = R y queda
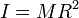
- Anillo circular
- Es un caso particular del anterior, pues el resultado no depende de la altura del cilindro
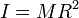
- Cilindro macizo
- Hacemos R1 = 0, R2 = R y resulta
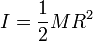
- Disco circular
- Es un caso particular del anterior