Péndulo compuesto
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se tiene un péndulo compuesto consistente en una barra de longitud <math>H</math> y masa <math>M</math> suspendida por un punto situado a una distancia <math>b</m…') |
(→Ecuaciones de movimiento) |
||
| Línea 4: | Línea 4: | ||
# Calcule la fuerza ejercida sobre el punto de anclaje cuando la barra pasa por la vertical en su oscilación. | # Calcule la fuerza ejercida sobre el punto de anclaje cuando la barra pasa por la vertical en su oscilación. | ||
==Ecuaciones de movimiento== | ==Ecuaciones de movimiento== | ||
| + | Determinaremos en primer lugar la ecuación de movimiento para el ángulo <math>\theta</math> que la barra forma con la vertical. | ||
| + | |||
| + | La barra constituye un sólido rígido sometido a dos fuerzas: | ||
| + | |||
| + | * Su peso, <math>M\vec{g}</math> | ||
| + | * La fuerza de reacción, <math>\Phi</math> ejercida por el soporte | ||
| + | |||
| + | La suma de estas dos fuerzas produce la aceleración del centro de masas | ||
| + | |||
| + | <center><math>M\vec{g}+\vec{\Phi} = M\vec{a}_C</math></center> | ||
| + | |||
| + | La suma de los momentos produce la variación del momento cinético de la partícula | ||
| + | |||
| + | <center><math>\vec{r}_C\times(M\vec{g})+\vec{r}_S\times\vec{\Phi} = \frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}</math></center> | ||
| + | |||
==Periodo== | ==Periodo== | ||
==Fuerza de reacción== | ==Fuerza de reacción== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 21:18 5 ene 2012
Contenido |
1 Enunciado
Se tiene un péndulo compuesto consistente en una barra de longitud H y masa M suspendida por un punto situado a una distancia b del centro de la barra (b < H / 2). Suponiendo que la barra se desvía un ángulo pequeño $\theta_0$ respecto de la vertical y a partir de ahí se suelta:
- Determine el periodo de oscilación de la barra
- Calcule la fuerza ejercida sobre el punto de anclaje cuando la barra pasa por la vertical en su oscilación.
2 Ecuaciones de movimiento
Determinaremos en primer lugar la ecuación de movimiento para el ángulo θ que la barra forma con la vertical.
La barra constituye un sólido rígido sometido a dos fuerzas:
- Su peso,
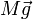
- La fuerza de reacción, Φ ejercida por el soporte
La suma de estas dos fuerzas produce la aceleración del centro de masas
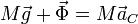
La suma de los momentos produce la variación del momento cinético de la partícula






