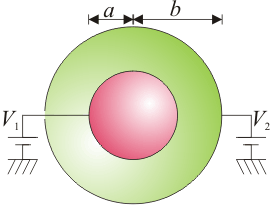
Conductores esféricos concéntricos

De Laplace

Revisión de 16:41 16 jul 2008 (ver código fuente) Antonio (Discusión | contribuciones) ← Edición más antigua		Revisión de 16:47 16 jul 2008 (ver código fuente) Antonio (Discusión | contribuciones) (→Solución) Edición más nueva →
Línea 8:		Línea 8:
	==Solución==		==Solución==
-	Este problema posee bastantes puntos en común con el de una sola esfera, en particular la simetría, por lo que se hará referencia a los resultados que allí se obtienen.	+	Este problema posee bastantes puntos en común con el de [[Capacidad de una esfera|una sola esfera]], en particular la simetría, por lo que se hará referencia a los resultados que allí se obtienen.
		+
		+	===Caso de dos potenciales fijados===
		+	Cuando tenemos superficies conductoras cerradas, cuyos potenciales son conocidos, los problemas se desacoplan en varios independientes. Cada conductor funciona como una [[jaula de Faraday]] separando el problema interior del exterior.
		+
		+	En este caso, en que tenemos dos superficies esféricas concéntricas, el espacio se divide en tres regiones:
		+
		+	====Región interior <math>(r<a)</math>====
		+
		+	====Región intermedia <math>(a<r<b)</math>====
		+
		+	====Región exterior <math>(r>b)</math>=====
		+
	[[Categoría:Problemas de campo eléctrico en presencia de conductores]]		[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

---

Revisión de 16:47 16 jul 2008

Contenido 1 Enunciado 2 Solución 2.1 Caso de dos potenciales fijados 2.1.1 Región interior (r < a) 2.1.2 Región intermedia (a < r < b) 2.1.3 Región exterior (r > b)=

1 Enunciado

Se tiene un sistema de dos conductores. Uno de ellos es una esfera metálica maciza de radio a. El otro es una fina corteza esférica metálica, de radio b, concéntrica con la anterior. Calcule el potencial en todos los puntos del espacio en los casos siguientes.

1. La esfera interior se encuentra a potencial V₁ y la exterior a potencial V₂.
2. La esfera interior almacena una carga Q₁ y la exterior una carga Q₂.
3. La esfera interior almacenada una carga Q₁ y la exterior se encuentra a un potencial V₂.
4. Calcule asimismo la energía almacenada en el sistema de dos esferas, para las tres situaciones indicadas.

2 Solución

Este problema posee bastantes puntos en común con el de una sola esfera, en particular la simetría, por lo que se hará referencia a los resultados que allí se obtienen.

2.1 Caso de dos potenciales fijados

Cuando tenemos superficies conductoras cerradas, cuyos potenciales son conocidos, los problemas se desacoplan en varios independientes. Cada conductor funciona como una jaula de Faraday separando el problema interior del exterior.

En este caso, en que tenemos dos superficies esféricas concéntricas, el espacio se divide en tres regiones:

2.1.1 Región interior (r < a)

2.1.2 Región intermedia (a < r < b)

2.1.3 Región exterior (r > b)=