Propulsión a reacción (GIE)
De Laplace
(Página creada con '==Enunciado== Un cohete a reacción se impulsa en el espacio emitiendo gases a cierta velocidad en el sentido opuesto a su propio movimiento. Sea un cohete que tiene una masa <…') |
|||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | [[Archivo:propulsion-chorro.jpg|right]] | |
| - | + | ||
| - | + | Una de las aplicaciones más inmediatas de la ley de conservación de la cantidad de movimiento para un sistema de partículas es el estudio de la propulsión a reacción o propulsión a chorro. | |
| - | + | ||
| - | + | En su versión más sencilla consiste en la expulsión de gases a gran velocidad por la tobera de un cohete de forma, que por la tercera ley de Newton, el cohete se ve acelerado en el sentido opuesto al de la expulsión. | |
| - | + | Este principio permite acelerar y maniobrar a las naves en el espacio (en el que no tienen dónde “apoyarse”), aunque en la mayoría del trayecto se mueven por inercia sometidas simplemente a los campos gravitatorios presentes. | |
| - | En el | + | En el caso de un avance en línea recta puede calcularse la cantidad de combustible necesaria para que una cierta carga alcance una velocidad deseada (por ejemplo, la [[velocidad de escape (GIE)|velocidad de escape]]. |
| - | + | Podemos resolver este problema, usando la ley de conservación de la cantidad de movimiento. | |
| - | + | Tenemos una nave que en un momento dado, incluyendo el combustible que contiene, tiene una masa <math>M</math> y se mueve a una velocidad <math>v</math>. En un intervalo de tiempo corto expulsa una cantidad de gases de masa <math>\mathrm{d}m</math>. Estos gases son eyectados con rapidez <math>v_0</math> respecto a la nave, de forma que su velocidad respecto a un observador exterior es <math>v-v_0</math>. Con la expulsión, la masa de la nave pasa a ser <math>M-\mathrm{d}m</math> y su velocidad <math>v+\mathrm{d}v</math>. | |
| - | + | La ecuación básica es que en dos instantes sucesivos la cantidad de movimiento del sistema nave+gas expulsado es la misma, y por tanto | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | La | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<center><math>M v = (M-\mathrm{d}m)(v+\mathrm{d}v) + (\mathrm{d}m)(v-v_0)\,</math></center> | <center><math>M v = (M-\mathrm{d}m)(v+\mathrm{d}v) + (\mathrm{d}m)(v-v_0)\,</math></center> | ||
| - | |||
| - | |||
Despejando e igualando queda | Despejando e igualando queda | ||
| Línea 81: | Línea 34: | ||
Integrando cada miembro | Integrando cada miembro | ||
| + | |||
| + | <center><math>-\int_{M_i}^{M_f}\frac{\mathrm{d}M}{M}=\frac{1}{v_0}\int_{0}^{v_f}\mathrm{d}v</math></center> | ||
| + | |||
| + | Debe observarse que la velocidad inicial de la nave no es <math>v_0</math> (que es la velocidad de escape de los gases), sino 0, ya que parte del reposo, y que <math>v_0</math> puede salir de la integral ya que se trata de una constante. Esto nos da | ||
<center><math>-\left.\ln M\right|_{M_i}^{M_f}=-\ln\left(\frac{M_f}{M_i}\right)=\frac{v_f}{v_0}</math></center> | <center><math>-\left.\ln M\right|_{M_i}^{M_f}=-\ln\left(\frac{M_f}{M_i}\right)=\frac{v_f}{v_0}</math></center> | ||
| Línea 88: | Línea 45: | ||
<center><math>v_f = v_0\ln\left(\frac{M_0+m_0}{M_0}\right)</math></center> | <center><math>v_f = v_0\ln\left(\frac{M_0+m_0}{M_0}\right)</math></center> | ||
| - | + | Esta es la llamada ecuación de Tsiolkovsky, básica en astronáutica. | |
| - | + | En este proceso no se conserva la energía cinética (lo cual es lógico, pues la nave se está acelerando). En un instante dado tenemos un cohete con masa <math>M</math> moviéndose a velocidad <math>v</math>, que tendrá energía cinética | |
| - | + | ||
| - | + | ||
| - | <center><math> | + | <center><math>K = \frac{1}{2}M v^2</math></center> |
| - | + | Un instante después tendremos gases moviéndose a velocidad <math>v-v_0</math> y la nave a velocidad <math>v+\mathrm{d}v</math> con lo que la nueva energía cinética es algo mayor que la anterior | |
| - | <center><math> | + | <center><math>K + \mathrm{d}K = \frac{1}{2}(M-\mathrm{d}m)(v+\mathrm{d}v)^2+\frac{1}{2}\mathrm{d}m(v-v_0)^2</math></center> |
| - | y | + | Restando y sustituyendo las relaciones anteriores queda el incremento de energía cinética |
| - | = | + | <center><math>\mathrm{d}K = \frac{1}{2}\mathrm{d}m\,v_0^2</math></center> |
| - | Si deseamos colocar una cierta cantidad de carga útil a una cierta velocidad, la cantidad de combustible necesaria se obtiene | + | |
| + | Esta energía extra sale de las reacciones químicas que tienen lugar al quemar el combustible. | ||
| + | |||
| + | Si deseamos colocar una cierta cantidad de carga útil (''payload'') a una cierta velocidad, la cantidad de combustible necesaria se obtiene despejando | ||
<center><math>m_0 = M_0\left(\mathrm{e}^{v_f/v_0}-1\right)\,</math></center> | <center><math>m_0 = M_0\left(\mathrm{e}^{v_f/v_0}-1\right)\,</math></center> | ||
| Línea 109: | Línea 67: | ||
Este crecimiento exponencial con la velocidad hace que sea muy importante optimizar la masa del cohete para reducir el combustible necesario. Por ello, los cohetes constan de fases, que se van desprendiendo a medida que dejan de ser necesarias. | Este crecimiento exponencial con la velocidad hace que sea muy importante optimizar la masa del cohete para reducir el combustible necesario. Por ello, los cohetes constan de fases, que se van desprendiendo a medida que dejan de ser necesarias. | ||
| - | = | + | Supongamos que se quiere poner sacar de la órbita terrestre un satélite de 1000 kg, mediante gases expulsados a 4 km/s. ¿Cuánto combustible hace falta para alcanzar la velocidad de escape de 11.2 km/s |
| + | |||
| + | <center><math>m_0 = (1000\,\mathrm{kg})(\mathrm{e}^{11.2/4}-1) \simeq 15000\,\mathrm{kg}</math></center> | ||
| + | Resultan 15 kilos de combustible por cada kg de ''payload''. Eso sin contar, por supuesto, el peso de la estructura del propio cohete, el trabajo extra para vencer la atracción gravitatoria y la fricción con el aire, que elevan la proporción de masa total respecto de carga útil. | ||
[[Categoría:Dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Dinámica de los sistemas de partículas (GIE)]] | ||
última version al 09:46 14 dic 2011
Una de las aplicaciones más inmediatas de la ley de conservación de la cantidad de movimiento para un sistema de partículas es el estudio de la propulsión a reacción o propulsión a chorro.
En su versión más sencilla consiste en la expulsión de gases a gran velocidad por la tobera de un cohete de forma, que por la tercera ley de Newton, el cohete se ve acelerado en el sentido opuesto al de la expulsión.
Este principio permite acelerar y maniobrar a las naves en el espacio (en el que no tienen dónde “apoyarse”), aunque en la mayoría del trayecto se mueven por inercia sometidas simplemente a los campos gravitatorios presentes.
En el caso de un avance en línea recta puede calcularse la cantidad de combustible necesaria para que una cierta carga alcance una velocidad deseada (por ejemplo, la velocidad de escape.
Podemos resolver este problema, usando la ley de conservación de la cantidad de movimiento.
Tenemos una nave que en un momento dado, incluyendo el combustible que contiene, tiene una masa M y se mueve a una velocidad v. En un intervalo de tiempo corto expulsa una cantidad de gases de masa dm. Estos gases son eyectados con rapidez v0 respecto a la nave, de forma que su velocidad respecto a un observador exterior es v − v0. Con la expulsión, la masa de la nave pasa a ser M − dm y su velocidad v + dv.
La ecuación básica es que en dos instantes sucesivos la cantidad de movimiento del sistema nave+gas expulsado es la misma, y por tanto
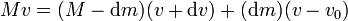
Despejando e igualando queda
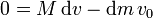
donde hemos despreciado el término 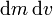 que es mucho más pequeño que los demás. Equivalentemente
que es mucho más pequeño que los demás. Equivalentemente
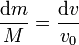
La cantidad de masa expulsada es igual a lo que disminuye la masa del cohete, por lo que
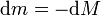
esto es

Integrando cada miembro

Debe observarse que la velocidad inicial de la nave no es v0 (que es la velocidad de escape de los gases), sino 0, ya que parte del reposo, y que v0 puede salir de la integral ya que se trata de una constante. Esto nos da
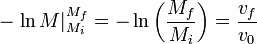
La masa inicial es la del cohete más el combustible, mientras que la del final es solo la del cohete, por lo que obtenemos finalmente
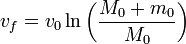
Esta es la llamada ecuación de Tsiolkovsky, básica en astronáutica.
En este proceso no se conserva la energía cinética (lo cual es lógico, pues la nave se está acelerando). En un instante dado tenemos un cohete con masa M moviéndose a velocidad v, que tendrá energía cinética
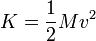
Un instante después tendremos gases moviéndose a velocidad v − v0 y la nave a velocidad v + dv con lo que la nueva energía cinética es algo mayor que la anterior
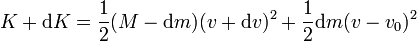
Restando y sustituyendo las relaciones anteriores queda el incremento de energía cinética
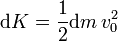
Esta energía extra sale de las reacciones químicas que tienen lugar al quemar el combustible.
Si deseamos colocar una cierta cantidad de carga útil (payload) a una cierta velocidad, la cantidad de combustible necesaria se obtiene despejando

Este crecimiento exponencial con la velocidad hace que sea muy importante optimizar la masa del cohete para reducir el combustible necesario. Por ello, los cohetes constan de fases, que se van desprendiendo a medida que dejan de ser necesarias.
Supongamos que se quiere poner sacar de la órbita terrestre un satélite de 1000 kg, mediante gases expulsados a 4 km/s. ¿Cuánto combustible hace falta para alcanzar la velocidad de escape de 11.2 km/s
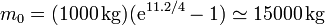
Resultan 15 kilos de combustible por cada kg de payload. Eso sin contar, por supuesto, el peso de la estructura del propio cohete, el trabajo extra para vencer la atracción gravitatoria y la fricción con el aire, que elevan la proporción de masa total respecto de carga útil.






