Entrar Página Discusión Historial Go to the site toolbox

Bloque entre dos placas conductoras

De Laplace

(Diferencias entre revisiones)
(→Carga en los condensadores)
(→Carga en los condensadores)
Línea 15: Línea 15:
En este sistema tenemos tres conductores: las dos placas y el bloque central.
En este sistema tenemos tres conductores: las dos placas y el bloque central.
-
La placa inferior (conductor “1”) se encuentra a potencial $V_0$; el bloque central (conductor ``2'') está aislado, pero almacena
+
La placa inferior (conductor &ldquo;1&rdquo;) se encuentra a potencial <math>V_0</math>; el bloque central (conductor &ldquo;2&rdquo;) está aislado, pero almacena una carga <math>Q_0</math>; la placa superior (conductor &ldquo;3&rdquo;) , que tomamos como referencia se encuentra a tierra.
-
una carga $Q_0$; la placa de la derecha (conductor ``3'') se encuentra
+
-
a tierra.
+
-
Los coeficientes de capacidad entre los distintos conductores son
+
Los coeficientes de capacidad entre los distintos conductores son inmediatos a partir del circuito equivalente: tenemos sendos condensadores entre el bloque y cada placa; dos fuentes de potencial (una de ellas a tierra) y una fuente de carga.
-
inmediatos a partir del circuito equivalente: tenemos sendos
+
 
-
condensadores entre el bloque y cada placa; dos fuentes de potencial
+
Nótese que los dos condensadores ''no están en serie'', por haber una carga acumulada en el bloque central. Para que dos condensadores estén en serie la carga de ambos debe ser la misma, cosa que no ocurre en este caso.
-
(una de ellas a tierra) y una fuente de carga.
+
-
\begin{center}
+
-
\includegraphics{doscond.eps}
+
-
\end{center}
+
-
Nótese que los dos condensadores \textbf{no están en serie}, por
+
-
haber una carga acumulada en el bloque central. Para que dos
+
-
condensadores estén en serie la carga de ambos debe ser la misma, cosa
+
-
que no ocurre en este caso.
+
Por tanto las capacidades del sistema no nulas son
Por tanto las capacidades del sistema no nulas son
-
\[
+
 
-
\overline{C}_{12}=\overline{C}_{23}=\frac{\varepsilon_0 S}{d} = \frac{\varepsilon_0
+
<center><math>\overline{C}_{12}=\overline{C}_{23}=\frac{\varepsilon_0 S}{d} = \frac{\varepsilon_0 L^2}{(b-a)}\equiv C</math></center>
-
L^2}{(b-a)}\equiv C
+
 
-
\]
+
y el resto se anula.
y el resto se anula.
De aquí obtenemos los coeficientes de capacidad
De aquí obtenemos los coeficientes de capacidad
-
\[
+
 
-
C_{11}=\overline{C}_{12}=C\qquad C_{12}=-\overline{C}_{12}=-C \qquad
+
<center><math>C_{11}=\overline{C}_{12}=C</math>{{qquad}}<math> C_{12}=-\overline{C}_{12}=-C</math>{{qquad}}<math>
-
C_{13}=0
+
C_{13}=0</math>{{qquad}}<math>
-
\]
+
C_{22}=\overline{C}_{12}+\overline{C}_{23}=2C</math>{{qquad}}<math>
-
\[
+
C_{23}=-\overline{C}_{23}=-C</math>{{qquad}}<math>C_{33}=\overline{C}_{23}=C</math></center>
-
C_{22}=\overline{C}_{12}+\overline{C}_{23}=2C\qquad
+
 
-
C_{23}=-\overline{C}_{23}=-C\qquad C_{33}=\overline{C}_{23}=C
+
-
\]
+
o, en forma matricial
o, en forma matricial
-
\[
+
 
-
\bsf{C}=C\pmatrix{1 & -1 & 0 \cr -1 & 2 & -1 \cr 0 & -1 & 1}
+
<center><math>\mathbf{\mathsf{C}=C\left(\begin{matrix}1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 1\end{matrix}\right)</math></center>
-
\]
+
 
La relación entre las cargas y potenciales será
La relación entre las cargas y potenciales será
-
\[
+
 
-
Q_1 = C(V_1-V_2)
+
<center><math>Q_1 = C(V_1-V_2)</math>{{qquad}}<math>Q_2=C(-V_1+2V_2 -V_3) = C(V_2-V_1) + C(V_2-V_3)</math>{{qquad}}<math>Q_3=C(V_3-V_2)</math></center>
-
\]
+
 
-
\[
+
Por supuesto, a este mismo resultado se podía haber llegado partiendo del circuito equivalente.
-
Q_2=C(-V_1+2V_2 -V_3) = C(V_2-V_1) + C(V_2-V_3)
+
-
\]
+
-
\[
+
-
Q_3=C(V_3-V_2)
+
-
\]
+
-
Por supuesto, a este mismo resultado se podía haber llegado partiendo
+
-
del circuito equivalente.
+
Sustituyendo los datos conocidos
Sustituyendo los datos conocidos
-
\[
+
 
-
V_1=V_0\qquad Q_2 = Q_0\qquad V_3 = 0
+
<center><math>V_1=V_0\,</math>{{qquad}}<math>Q_2 = Q_0\,</math>{{qquad}}<math>V_3 = 0\,</math></center>
-
\]
+
 
resulta la solución
resulta la solución
-
\[
+
 
-
V_2 = \frac{Q_0}{2C}+\frac{V_0}{2} \qquad
+
<center><math>V_2 = \frac{Q_0}{2C}+\frac{V_0}{2}</math>{{qquad}}
-
%\]\[
+
<math>Q_1 = \frac{CV_0}{2}-\frac{Q_0}{2}</math>{{qquad}}
-
Q_1 = \frac{CV_0}{2}-\frac{Q_0}{2} \qquad
+
<math>Q_3 = -\frac{CV_0}{2}-\frac{Q_0}{2}</math></center>
-
%\]\[
+
 
-
Q_3 = -\frac{CV_0}{2}-\frac{Q_0}{2}
+
Nótese que las cargas y potenciales dependen tanto de la diferencia de potencial como de la carga del bloque central.
-
\]
+
-
Nótese que las cargas y potenciales dependen tanto de la diferencia de
+
-
potencial como de la carga del bloque central.
+
===Energía almacenada===
===Energía almacenada===

Revisión de 13:25 16 jul 2008

Contenido

1 Enunciado

Dos placas conductoras planas y paralelas cuadradas, de lado L, se encuentran separadas una distancia 2b (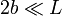2b\ll L). Entre ellas, y equidistante de ambas se encuentra un prisma conductor de anchura 2a, también de sección cuadrada de lado L.

El bloque posee una carga total Q0. Entre las placas se establece una diferencia de potencial V0

  1. Calcule la carga en cada uno de los condensadores que forma el bloque con las placas.
  2. Halle la energía almacenada en el sistema.
  3. Calcule el valor del campo en cada uno de los espacios intermedios entre bloque y placas.
  4. Halle la presión electrostática sobre las caras del bloque, así como la fuerza total sobre éste.
  5. Calcule los valores numéricos de los resultados anteriores para L = 2cm, a = 2mm, b = 3mm, V0 = 100V, Q0 = 10nC.

2 Solución

2.1 Carga en los condensadores

En este sistema tenemos tres conductores: las dos placas y el bloque central.

La placa inferior (conductor “1”) se encuentra a potencial V0; el bloque central (conductor “2”) está aislado, pero almacena una carga Q0; la placa superior (conductor “3”) , que tomamos como referencia se encuentra a tierra.

Los coeficientes de capacidad entre los distintos conductores son inmediatos a partir del circuito equivalente: tenemos sendos condensadores entre el bloque y cada placa; dos fuentes de potencial (una de ellas a tierra) y una fuente de carga.

Nótese que los dos condensadores no están en serie, por haber una carga acumulada en el bloque central. Para que dos condensadores estén en serie la carga de ambos debe ser la misma, cosa que no ocurre en este caso.

Por tanto las capacidades del sistema no nulas son

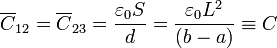
\overline{C}_{12}=\overline{C}_{23}=\frac{\varepsilon_0 S}{d} = \frac{\varepsilon_0 L^2}{(b-a)}\equiv C

y el resto se anula.

De aquí obtenemos los coeficientes de capacidad

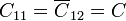
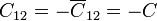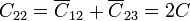
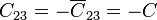
C_{11}=\overline{C}_{12}=C     C_{12}=-\overline{C}_{12}=-C    C13 = 0     C_{22}=\overline{C}_{12}+\overline{C}_{23}=2C     C_{23}=-\overline{C}_{23}=-C    C_{33}=\overline{C}_{23}=C

o, en forma matricial

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathbf{\mathsf{C}=C\left(\begin{matrix}1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 1\end{matrix}\right)

La relación entre las cargas y potenciales será

Q1 = C(V1 − V2)    Q2 = C( − V1 + 2V2 − V3) = C(V2 − V1) + C(V2 − V3)    Q3 = C(V3 − V2)

Por supuesto, a este mismo resultado se podía haber llegado partiendo del circuito equivalente.

Sustituyendo los datos conocidos

V_1=V_0\,    Q_2 = Q_0\,    V_3 = 0\,

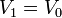
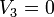
resulta la solución

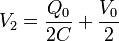
V_2 = \frac{Q_0}{2C}+\frac{V_0}{2}    

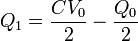
Q_1 = \frac{CV_0}{2}-\frac{Q_0}{2}    

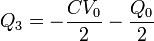
Q_3 = -\frac{CV_0}{2}-\frac{Q_0}{2}

Nótese que las cargas y potenciales dependen tanto de la diferencia de potencial como de la carga del bloque central.

2.2 Energía almacenada

2.3 Campo entre el bloque y las placas

2.4 Presión sobre el bloque

2.5 Valores numéricos

Obtenido de "http://tesla.us.es/wiki/index.php/Bloque_entre_dos_placas_conductoras"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace