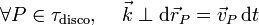Disco desenrollándose de una cuerda (G.I.A.)

De Laplace

(Diferencias entre revisiones)

Revisión de 14:33 9 dic 2011

1 Enunciado

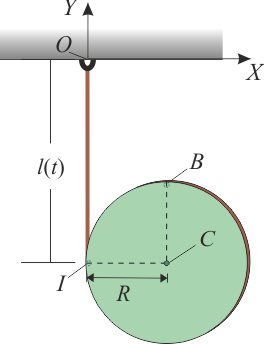
Un disco de radio

R

gira y cae, siempre contenido en el plano vertical

O X Y

, mientras se desenrrolla de una cuerda que pende verticalmente, y cuya longitud aumenta según la ley horaria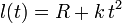 $l(t)=R+k\!\ t^2$ (donde

k

es una constante conocida).

Obtenga la reducción cinemática que describe el movimiento instantáneo del disco.
Velocidad y aceleración instantáneas del punto $B$ indicado en la figura.

2 Solución

2.1 Reducción cinemática del movimiento instantáneo

Como sabemos, el movimiento del disco respecto del sistema de referencia fijo queda caracterizado en cada instante por los dos vectores que forman la reducción cinemática: el vector rotación instantánea $\vec{\omega}$ y la velocidad de un punto cualquiera de dicho sólido. En el sistema bajo estudio, en que el disco se mueve siempre contenido en el plano $O X Y$ , hay un punto cuya velocidad instantánea es fácil de determinar: se trata del centro del disco $C$ , que se moverá siempre paralelo a la cuerda desenrollada (y, por tanto, al eje $O Y$ ), y según la ley horaria $l (t)$ . Es decir, proponemos la reducción cinemática

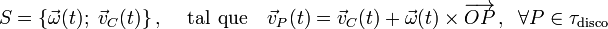
$S=\{\vec{\omega}(t);\ \vec{v}_C(t)\}\,\mathrm{,}\,\quad\,\mathrm{tal}\;\,\mathrm{que} \quad\vec{v}_P(t)=\vec{v}_C(t)+\vec{\omega}(t)\times\overrightarrow{OP}\,\mathrm{,}\;\;\,\forall P\in\tau_{\mathrm{disco}}$

Comencemos determinado la expresión instantánea de la velocidad del centro del disco. En todo instante, el radio-vector 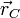$\vec{r}_C$ que determina la posición del centro $C$ respecto del punto fijo $O$ , adoptado como origen del sistema de referencia, puede expresarse como sigue:

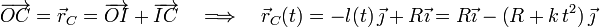
$\overrightarrow{OC}=\vec{r}_C=\overrightarrow{OI}+\overrightarrow{IC}\quad\Longrightarrow\quad\vec{r}_C(t)=-l(t)\!\ \vec{\jmath}+R\vec{\imath}=R\vec{\imath}-\big(R+k\!\ t^2\big)\!\ \vec{\jmath}$

siendo $I$ el punto geométrico donde la cuerda desenrrollada se separa del disco. La derivada temporal de las ecuaciones horarias que describen el movimiento del centro del disco, nos proporciona la expresión que indica cómo es, en el transcurso del tiempo, la velocidad instantánea de dicho punto:

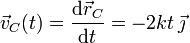
$\vec{v}_C(t)=\frac{\mathrm{d}\vec{r}_C}{\mathrm{d}t}=-2kt\!\ \vec{\jmath}$

Para obtener el vector rotación instantánea, comenzaremos por determinar su dirección. Para ello utilizaremos la informació de que el disco se mueve siempre contendio en el plano $O X Y$ . En consecuencia, los desplazamientos instantáneos de todos los punos del disco, en cualquier instante, punto del disco deben estar contenidos en dicho plano, olo que es lo mismo, deben ser perpendiculares al unitario $\vec{k}$ que indica la dirección del eje $O Z$ :

$\forall P\in\tau_{\mathrm{disco}},\quad \,\vec{k}\perp\mathrm{d}\vec{r}_P=\vec{v}_P\!\ \mathrm{d}t$

Revisión de 14:32 9 dic 2011 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Reducción cinemática del movimiento instantáneo) ← Edición más antigua		Revisión de 14:33 9 dic 2011 (ver código fuente) Gabriel (Discusión \| contribuciones) (→Reducción cinemática del movimiento instantáneo) Edición más nueva →
Línea 21:		Línea 21:
	Para obtener el vector rotación instantánea, comenzaremos por determinar su dirección. Para ello utilizaremos la informació de que el disco se mueve siempre contendio en el plano <math>OXY</math>. En consecuencia, los desplazamientos instantáneos de todos los punos del disco, en cualquier instante, punto del disco deben estar contenidos en dicho plano, olo que es lo mismo, deben ser perpendiculares al unitario <math>\vec{k}</math> que indica la dirección del eje <math>OZ</math>:		Para obtener el vector rotación instantánea, comenzaremos por determinar su dirección. Para ello utilizaremos la informació de que el disco se mueve siempre contendio en el plano <math>OXY</math>. En consecuencia, los desplazamientos instantáneos de todos los punos del disco, en cualquier instante, punto del disco deben estar contenidos en dicho plano, olo que es lo mismo, deben ser perpendiculares al unitario <math>\vec{k}</math> que indica la dirección del eje <math>OZ</math>:

-	<center><math>\forall P\in\tau_{\mathrm{disco}},\quad \,\mathrm{d}\vec{r}_P=\vec{v}_P\!\ \mathrm{d}t~~\ \perp\ \vec{k}~~</math></center>	+	<center><math>\forall P\in\tau_{\mathrm{disco}},\quad \,\vec{k}\perp\mathrm{d}\vec{r}_P=\vec{v}_P\!\ \mathrm{d}t</math></center>

Disco desenrollándose de una cuerda (G.I.A.)

De Laplace

Revisión de 14:33 9 dic 2011

1 Enunciado

2 Solución

2.1 Reducción cinemática del movimiento instantáneo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES