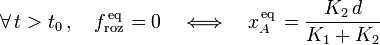Cuestión de equilibrio estático, Noviembre 2011

De Laplace

(Diferencias entre revisiones)

Revisión de 20:51 30 nov 2011

Contenido

1 Enunciado
2 Solución
- 2.1 Equilibrio en el caso de vínculos lisos
  - 2.1.1 Para el punto sin masa A
  - 2.1.2 Para el punto pesado B
- 2.2 Equilibrio en el caso de rozamiento en A
  - 2.2.1 Para el punto sin masa A

1 Enunciado

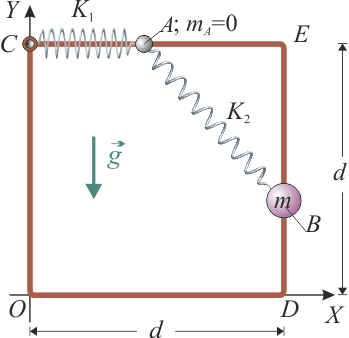
Cuatro varillas de igual longitud

d

están dispuestas formando un cuadrado

O D E C

, contenido en el plano vertical

O X Y

. Un resorte de longitud natural nula y constante recuperadora

K 1

conecta el vértice fijo

C

del cuadrilátero con un punto

A

de masa despreciable que puede desplazarse a lo largo de la varilla horizontal superior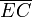 $\overline{EC}$ . Además, una partícula material

B

, cuya masa tiene un valor

m

está insertada en el lado vertical 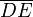$\overline{DE}$ de manera que su movimiento está limitado a desplazamientos sobre dicha varilla. Un segundo resorte de longitud natural nula y constante recuperadora

K 2

conecta la partícula

B

al punto

A

. Los valores de los parámetros del sistema son tales que

K 2 d > m g

.

Considerando que los vínculos son perfectamente lisos, determine las posiciones de equilibrio de las partículas $A$ y $B$ .
Considérese ahora que, mientras que el vínculo en $B$ sigue siendo liso, la partícula sin masa $A$ está sometida a un vínculo rugoso cuya fuerza de rozamiento verifica las leyes del rozamiento seco. ¿Cuáles son las posiciones de equilibrio?

2 Solución

2.1 Equilibrio en el caso de vínculos lisos

2.1.1 Para el punto sin masa $A$

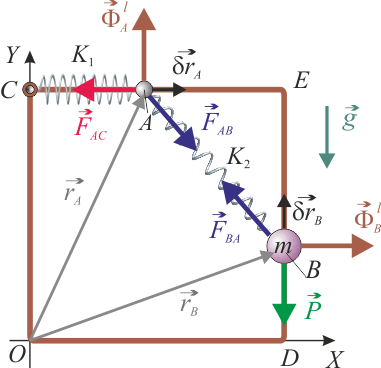
En la figura se muestra el diagrama de fuerzas que actúan sobre cada una de las partículas susceptibles de moverse en el sistema. Como la partícula $A$ no tiene masa, tampoco habrá una fuerza peso actuando sobre ella y sólo estará sometida a la acción del resorte $K 1$ más la acción del vínculo geométrico liso que sólo le permite moverse a lo largo del lado 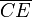$\overline{CE}$ . De esta forma, la descripción analítica de una posición arbitraria del punto $A$ , será:

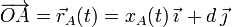
$\overrightarrow{OA}=\vec{r}_A(t)=x_A(t)\!\ \vec{\imath}\!\ + d\!\ \vec{\jmath}$

Comos sabemos, esta acción puede modelarse mediante una fuerza de reacción vincular equivalente, que denominaremos 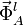$\vec{\Phi}_A^l$ , y que debe ser perpendicular al desplazamiento permitido de la partícula $A$ . Según el sistema de refererencia cartesiano que estamos utilizando, se tendrá:

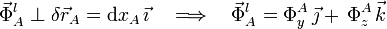
$\vec{\Phi}_A^l\perp\delta\vec{r}_A=\mathrm{d} x_A\!\ \vec{\imath}\quad\Longrightarrow\quad\vec{\Phi}_A^l=\Phi_y^A\!\ \vec{\jmath}+\!\ \Phi_z^A\!\ \vec{k}$

El resorte $K 1$ , de longitud natural nula y con un extremo fijo en $C$ , ejerce sobre $A$ una fuerza con la dirección y el sentido del segmento 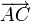$\overrightarrow{AC}$ , y proporcional a su longitud:

$\vec{F}_{AC}=K_1\overrightarrow{AC}=-K_1\!\ x_A(t)\!\ \vec{\imath}=\vec{F}_1$

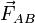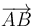Pero también el resorte $K 2$ actúa sobre esta partícula sin masa con una fuerza que denominaremos $\vec{F}_{AB}$ . Como su longitud natural es nula y tine su otro extremo conectado a la partícula $B$ , la correspondiente fuerza será propocional y con igual dirección y sentido que el segmento orientado $\overrightarrow{AB}$ .

$\vec{F}_{AB}=K_2\overrightarrow{AB}=K_2\big[\vec{r}_B(t)-\vec{r}_A(t)\big]$

Es decir, el valor de esta fuerza depende la posición del punto $B$ . Como, por la acción de un vínculo geométrico liso, éste está obligado a desplazarse siempre sobre el lado vertical 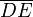$\overline{DE}$ , se tendrá:

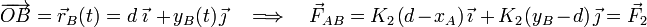
$\overrightarrow{OB}=\vec{r}_B(t)=d\ \vec{\imath}\ + y_B(t)\!\ \vec{\jmath}\quad\Longrightarrow\quad\vec{F}_{AB}=K_2\!\ \big(d-x_A\big)\!\ \vec{\imath}\ + K_2\!\ \big(y_B-d\big)\!\ \vec{\jmath}=\vec{F}_2$

Una vez determinadas todas las fuerzas que actúan sobre la partícula $A$ , podemos establecer las condiciones para que ésta se encuentre en equilibrio estático; es decir, para que se mantenga en una posición fija. Como sabemos, para que esto ocurra es necesario que se anule la resultante de todas las fuerzas que actúan sobre la partícula:

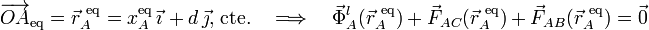
$\overrightarrow{OA}_\mathrm{eq}=\vec{r}_A^{\ \mathrm{eq}}=x_A^\mathrm{eq}\!\ \vec{\imath}\!\ + d\!\ \vec{\jmath}\mathrm{,}\; \mathrm{cte.}\quad\Longrightarrow\quad\vec{\Phi}_A^l(\vec{r}_A^{\ \mathrm{eq}})+\vec{F}_{AC}(\vec{r}_A^{\ \mathrm{eq}})+\vec{F}_{AB}(\vec{r}_A^{\ \mathrm{eq}})=\vec{0}$

Proyectando esta ecuación vectorial en las tres direcciones cartesianas, obtendremos la posición de equilibrio para el punto $A$ , así como las componentes de la fuerza de reacción vincular que actúa sobre dicho punto sin masa:

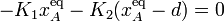
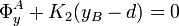
$\displaystyle-K_1x_A^\mathrm{eq}-K_2(x_A^\mathrm{eq}-d)=0$ $\Rightarrow$ $\displaystyle x_A^\mathrm{eq}=\frac{K_2}{K_1+K_2}\ d$

$\displaystyle\Phi_y^A+K_2(y_B-d)=0$ $\Rightarrow$ $\displaystyle \Phi_y^A\big\rfloor_{\vec{r}_A^{\ \mathrm{eq}}}=K_2\big[\ d-y_B(t)\ \big]$

$\Phi_z^A\big\rfloor_{\vec{r}_A^{\ \mathrm{eq}}}=0$

Estos resultados indican que la posición de equilibrio del punto $A$ (su coordenada 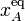$x_A^\mathrm{eq}$ , ya que $y A = d$ , al estar vinculada por el lado 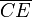$\overline{CE}$ ) SÓLO DEPENDE de los valores de las constantes recuperadoras de los muelles, $K 1$ y $K 2$ . Obsérvese que la partícula $A$ estará en equilibrio en dicha posición sea cual sea la masa o la posición de la partícula $B$ . Incluso, esta partícula puede estar en movimiento, pero $A$ estaría en reposo en la posición de equilibrio que hemos determinado. La segunda de las anteriores ecuaciones nos indica que la fuerza de reacción vincular en el punto $A$ , sí va a depender de la posición de $B$ e, indirectamente, de su masa.

2.1.2 Para el punto pesado $B$

Pasemos a analizar el equilibrio de la partícula pesada $B$ . Las fuerzas activas que actúan sobre ella son la fuerza peso y el resorte de constante recuperadora $K 2$ . Este último ejercerá una fuerza 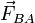$\vec{F}_{BA}$ que, por el principio de acción y reacción, tendrá igual dirección y módulo que 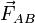$\vec{F}_{AB}$ , pero actuando en sentido contrario. Tendremos por tanto:

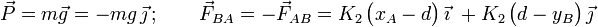
$\vec{P}=m\vec{g}=-mg\!\ \vec{\jmath}\,\mathrm{;}\,\qquad\vec{F}_{BA}=-\vec{F}_{AB}=K_2\!\ \big(x_A-d\big)\!\ \vec{\imath}\ + K_2\!\ \big(d-y_B\big)\!\ \vec{\jmath}$

Como ya sabemos, el punto material está obligado a moverse a lo largo del lado 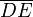$\overline{DE}$ , de manera que su coordenada $x B$ tiene un valor constante $d$ , mientras que la $y B$ camibará cuando la partícula se mueva. Introducimos una fuerza de reacción vincular 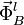$\vec{\Phi}_B^l$ equivalente a este vínculo geométrico liso:

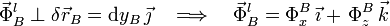
$\vec{\Phi}_B^l\perp\delta\vec{r}_B=\mathrm{d} y_B\!\ \vec{\jmath}\quad\Longrightarrow\quad\vec{\Phi}_B^l=\Phi_x^B\!\ \vec{\imath}+\!\ \Phi_z^B\!\ \vec{k}$

Para que $B$ se halle en equilibrio es condición necesaria que estas fuerzas se anulen entre sí...

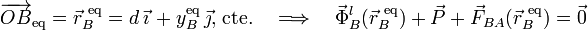
$\overrightarrow{OB}_\mathrm{eq}=\vec{r}_B^{\ \mathrm{eq}}=d\!\ \vec{\imath}\!\ + y_B^\mathrm{eq}\!\ \vec{\jmath}\mathrm{,}\; \mathrm{cte.}\quad\Longrightarrow\quad\vec{\Phi}_B^l(\vec{r}_B^{\ \mathrm{eq}})+\vec{P}+\vec{F}_{BA}(\vec{r}_B^{\ \mathrm{eq}})=\vec{0}$

... y ya podemos determinar las coordenadas de la posición de equilibrio de $B$ y el valor de la fuerza de reacción vincular:

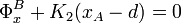
$\displaystyle\Phi_x^B+K_2(x_A-d)=0$ $\Rightarrow$ $\displaystyle \Phi_x^B\big\rfloor_{\vec{r}_B^{\ \mathrm{eq}}}=K_2\big[\ d-x_A(t)\ \big]=0$

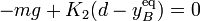
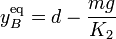
$\displaystyle-mg+K_2(d-y_B^\mathrm{eq})=0$ $\Rightarrow$ $\displaystyle y_B^\mathrm{eq}=d-\frac{mg}{K_2}$

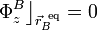
$\Phi_z^B\big\rfloor_{\vec{r}_B^{\ \mathrm{eq}}}=0$

En este caso, la posición de equilibrio de $B$ sólo depende de su propia masa y de las características del resorte al que está conectado (es decir, de $K 2$ ). Es decir, es independiente de la posición que ocupe la partícula $A$ , incluso del estado cinemático de ésta y, por tanto, no se ve afectada por el resorte $K 1$ . Nótese que, dada la relación que guardan los parámetros físicos del sistema, podemos asegurar que la partícula $B$ se encontrará en equilibrio en algún punto del lado vertical 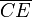$\overline{CE}$ , pero excluyendo sus extremos:

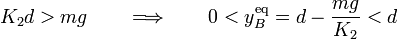
$\displaystyle K_2 d> mg\qquad\Longrightarrow\qquad 0<y_B^\mathrm{eq}=d-\frac{mg}{K_2}<d$

Por otra parte, la fuerza de reacción vincular en $B$ sí va a depender de la posición que en un determinado instante puede ocupar la partícula sin masa, $A [x A (t), d]$ .

2.2 Equilibrio en el caso de rozamiento en $A$

2.2.1 Para el punto sin masa $A$

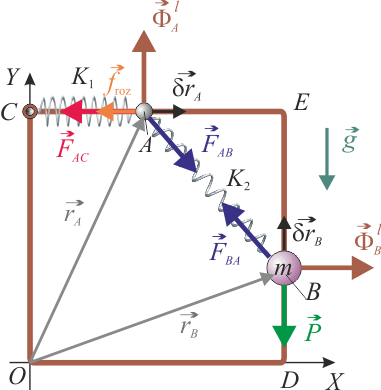
Ahora, la partícula sin masa $A$ va a estar sometida a un vínculo rugoso que, además del vínculo geométrico considerado en el apartado 2.1.1, incorpora una fuerza que cumple las leyes del rozamiento seco:

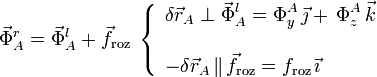
$\vec{\Phi}_A^r=\vec{\Phi}_A^l+\vec{f}_\mathrm{roz}\;\left\{\begin{array}{l}\displaystyle\delta\vec{r}_A\perp\vec{\Phi}_A^l=\Phi_y^A\!\ \vec{\jmath}+\!\ \Phi_z^A\!\ \vec{k}\\ \\ \displaystyle -\delta\vec{r}_A \!\ \|\!\ \vec{f}_\mathrm{roz}=f_\mathrm{roz}\!\ \vec{\imath}\end{array}\right.$

donde el signo de $f roz$ indicará el sentido de la fuerza de rozamiento. El resto de fuerzas que actúan sobre $A$ son las mismas que se describieron en el caso de vínculo liso. Nuevamente, la posición de equilibrio de dicho punto está sometida a la condición:

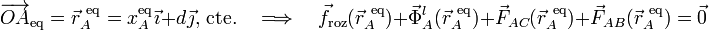
$\overrightarrow{OA}_\mathrm{eq}=\vec{r}_A^{\ \mathrm{eq}}=x_A^\mathrm{eq}\!\ \vec{\imath}\!\ + d\!\ \vec{\jmath}\mathrm{,}\; \mathrm{cte.}\quad\Longrightarrow\quad\vec{f}_\mathrm{roz}(\vec{r}_A^{\ \mathrm{eq}})+\vec{\Phi}_A^l(\vec{r}_A^{\ \mathrm{eq}})+\vec{F}_{AC}(\vec{r}_A^{\ \mathrm{eq}})+\vec{F}_{AB}(\vec{r}_A^{\ \mathrm{eq}})=\vec{0}$

Hay una nueva fuerza, que modificará la ecuación correspondiente a la proyección de esta ecuación vectorial en la dirección del eje $O X$ :

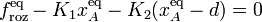
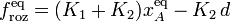
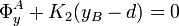
$\displaystyle f_\mathrm{roz}^\mathrm{eq}-K_1x_A^\mathrm{eq}-K_2(x_A^\mathrm{eq}-d)=0$ $\Rightarrow$ $\displaystyle f_\mathrm{roz}^\mathrm{eq}=(K_1+K_2)x_A^\mathrm{eq}-K_2\!\ d$

$\displaystyle\Phi_y^A+K_2(y_B-d)=0$ $\Rightarrow$ $\displaystyle \Phi_y^A\big\rfloor_{\vec{r}_A^{\ \mathrm{eq}}}=K_2\big[\ d-y_B(t)\ \big]$

$\Phi_z^A\big\rfloor_{\vec{r}_A^{\ \mathrm{eq}}}=0$

Como sabemos, si la partícula se encuentra en equilibrio estático, el módulo de la fuerza de rozamiento no puede superar un valor límite que depende de la naturaleza del contacto (caracterizado por valor del coeficiente de rozamiento estático $μ e$ ), y del módulo de la fuerza de reacción que modela el vínculo geométrico:

$\displaystyle |f_\mathrm{roz}^{\,\mathrm{eq}\,}|\leq\mu_e\!\ |\vec{\Phi}_A^l(\vec{r}_A^{\ \mathrm{eq}})|=\mu_e\!\ K_2\big[\ d-y_B(t)\ \big]$

Si combinamos esta desigualdad con la primera de las tres ecuaciones algebraicas que proporciona la condición equilibrio, obtenemos que la partícula $A$ se encontrará en equilibrio en un rango de valores de $x a$ en torno a la posición de equilibrio que obtuvimos en ausencia de rozamiento:

$\displaystyle \frac{K_2\!\ d}{K_1+K_2}-\Delta x\!\ \leq x_A^\mathrm{eq}\leq\!\ \frac{K_2\!\ d}{K_1+K_2}+\Delta x$ $\,\mathrm{con}\,\quad\Delta x=\frac{\mu_e\!\ K_2}{K_1+K_2}\ \big[\!\ d - y_B\!\ \big]$

Obsérvese que la anchura del rango o intervalo de posiciones en que $A$ se mantendrá en equilibrio, sí va a depender de la posición de $B$ , siendo más ancho cuanto más abajo se encuentre esta partícula y cuanto mayor sea el coeficiente de rozamiento estático en el punto $A$ .

Por otra parte, nótese que si el punto $B$ no está en equilibrio (es decir, $y B = y B (t)$ ), el tamaño del rango de posiciones de equilibrio variará en el tiempo. Si en un determinado instante $t 0$ , la partícula $B$ alcanzase el punto $E$ , se tendría...

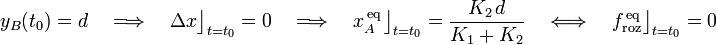
$y_B(t_0)=d\quad\Longrightarrow\quad \Delta x\big\rfloor_{t= t_0}=0 \quad\Longrightarrow\quad x_A^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=\frac{K_2\!\ d}{K_1+K_2}\quad\Longleftrightarrow\quad f_\mathrm{roz}^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=0$

Es decir, al anularse la anchura de su intervalo de equilibrio, la partícula $A$ se desplazaría hacia la única posición de equilibrio posible: la correspondiente al caso sin rozamiento. Pero, una vez allí, la fuerza de rozamiento desaparece por lo que, ésta sería también la única posición de equilibrio posible en cualquier instante posterior:

$\forall\, t>t_0\,\mathrm{,}\,\quad f_\mathrm{roz}^{\,\mathrm{eq}\,}=0\quad\Longleftrightarrow\quad x_A^{\,\mathrm{eq}\,}=\frac{K_2\!\ d}{K_1+K_2}$

@@ Línea 115: / Línea 115: @@
 <center><math>y_B(t_0)=d\quad\Longrightarrow\quad \Delta x\big\rfloor_{t= t_0}=0
-\quad\Longleftrightarrow\quad x_A^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=\frac{K_2\!\ d}{K_1+K_2}\quad\Longleftrightarrow\quad f_\mathrm{roz}^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=0</math></center>
+\quad\Longrightarrow\quad x_A^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=\frac{K_2\!\ d}{K_1+K_2}\quad\Longleftrightarrow\quad f_\mathrm{roz}^{\,\mathrm{eq}\,}\big\rfloor_{t= t_0}=0</math></center>
 Es decir, al anularse la anchura de su intervalo de  equilibrio, la partícula <math>A</math> se desplazaría hacia la única posición de equilibrio posible: la correspondiente al caso sin rozamiento. Pero, una vez allí, la fuerza de rozamiento desaparece por lo que, ésta sería también la única posición de equilibrio posible en cualquier instante posterior:

Cuestión de equilibrio estático, Noviembre 2011

De Laplace

Revisión de 20:51 30 nov 2011

Contenido

1 Enunciado

2 Solución

2.1 Equilibrio en el caso de vínculos lisos

2.1.1 Para el punto sin masa $A$

2.1.2 Para el punto pesado $B$

2.2 Equilibrio en el caso de rozamiento en $A$

2.2.1 Para el punto sin masa $A$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Cuestión de equilibrio estático, Noviembre 2011

De Laplace

Revisión de 20:51 30 nov 2011

Contenido

1 Enunciado

2 Solución

2.1 Equilibrio en el caso de vínculos lisos

2.1.1 Para el punto sin masa A

2.1.2 Para el punto pesado B

2.2 Equilibrio en el caso de rozamiento en A

2.2.1 Para el punto sin masa A

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1.1 Para el punto sin masa $A$

2.1.2 Para el punto pesado $B$

2.2 Equilibrio en el caso de rozamiento en $A$

2.2.1 Para el punto sin masa $A$