Fuerza en anilla ensartada en varillas
De Laplace
| Línea 5: | Línea 5: | ||
==Sin considerar el peso== | ==Sin considerar el peso== | ||
| - | [[Anilla_ensartada_en_dos_varillas_(GIE)| | + | Conocemos el movimiento de la anilla; se ve en [[Anilla_ensartada_en_dos_varillas_(GIE)|este problema]] y en [[Ejemplo_de_movimiento_expresado_en_polares|este otro]]: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular <math>2\Omega</math> y el radio de giro <math>L/2</math>. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda, |
<center><math>\vec{r}(t) = L\cos^2(\Omega t)\vec{\imath}+L\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{\jmath}</math></center> | <center><math>\vec{r}(t) = L\cos^2(\Omega t)\vec{\imath}+L\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{\jmath}</math></center> | ||
| Línea 15: | Línea 15: | ||
Podemos hallar esta aceleración derivando dos veces la ecuación anterior. Sin embargo, es más simple aprovechar el que sabemos que describe un movimiento circular uniforme, por lo que su aceleración es igual a | Podemos hallar esta aceleración derivando dos veces la ecuación anterior. Sin embargo, es más simple aprovechar el que sabemos que describe un movimiento circular uniforme, por lo que su aceleración es igual a | ||
| - | <center><math>\vec{a} = -\omega^2(\vec{r}-\vec{r}_c)= | + | <center><math>\vec{a} = -\omega^2(\vec{r}-\vec{r}_c)=(2\Omega)^2\left(\frac{L}{2}\right)\vec{N}=2\Omega^2L\vec{N}</math></center> |
| - | siendo <math>\vec{ | + | siendo <math>\vec{N}</math> el vector unitario radial desde la anilla hacia el centro de la circunferencia que describe. |
Por tanto, la fuerza neta será igual a | Por tanto, la fuerza neta será igual a | ||
| - | <center><math>\vec{F}=-2m\Omega^2L\vec{ | + | <center><math>\vec{F}=2m\Omega^2L\vec{N}</math></center> |
| + | |||
| + | Esta fuerza es la resultante de las fuerzas ejercidas por cada una de las barras. Éstas pueden empujar a la anilla lateralmente, pero no pueden impedir que se deslice a lo largo; por tanto, la fuerza que ejerce cada una es perpendicular a la propia barra. | ||
| + | |||
| + | Tenemos entonces que descomponer la fuerza neta en suma vectorial de dos fuerzas, cada una de ellas perpendicular a la barra que la ejerce. Dado que para esta geometría en concreto las dos varillas son perpendiculares entre sí, quiere decir que la fuerza que ejerce la barra 1 va en la dirección de la 2 y viceversa. | ||
| + | |||
| + | El ángulo que forma el vector <math>\vec{N}</math> con la barra de la izquierda nos lo da el que el triángulo OCP es isósceles. Por tanto, el ángulo buscado es igual a <math>\theta = \Omega t</math>. El ángulo que forma con la segunda barra será su complementario, <math>\pi/2-\theta</math>. Los módulos de las dos fuerzas valen entonces | ||
| + | |||
| + | <center><math>|\vec{F}_1| = |\vec{F}|\cos(\theta) = 2m\Omega^2L\cos(\Omega t)\qquad\qquad |\vec{F}_2| = |\vec{F}|\mathrm{sen}(\theta) = 2m\Omega^2L\,\mathrm{sen}(\Omega t)</math></center> | ||
==Incluyendo el peso== | ==Incluyendo el peso== | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 11:09 26 nov 2011
1 Enunciado
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ´esta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.
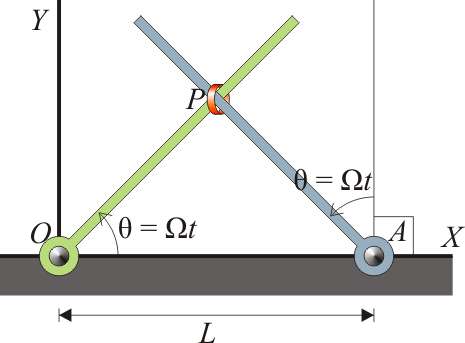
2 Sin considerar el peso
Conocemos el movimiento de la anilla; se ve en este problema y en este otro: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular 2Ω y el radio de giro L / 2. La ecuación horaria del movimiento es, respecto al anclaje de la izquierda,
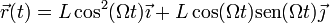
La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton
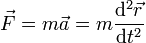
Podemos hallar esta aceleración derivando dos veces la ecuación anterior. Sin embargo, es más simple aprovechar el que sabemos que describe un movimiento circular uniforme, por lo que su aceleración es igual a
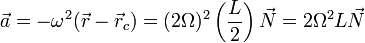
siendo 
el vector unitario radial desde la anilla hacia el centro de la circunferencia que describe.
Por tanto, la fuerza neta será igual a
Esta fuerza es la resultante de las fuerzas ejercidas por cada una de las barras. Éstas pueden empujar a la anilla lateralmente, pero no pueden impedir que se deslice a lo largo; por tanto, la fuerza que ejerce cada una es perpendicular a la propia barra.
Tenemos entonces que descomponer la fuerza neta en suma vectorial de dos fuerzas, cada una de ellas perpendicular a la barra que la ejerce. Dado que para esta geometría en concreto las dos varillas son perpendiculares entre sí, quiere decir que la fuerza que ejerce la barra 1 va en la dirección de la 2 y viceversa.
El ángulo que forma el vector con la barra de la izquierda nos lo da el que el triángulo OCP es isósceles. Por tanto, el ángulo buscado es igual a θ = Ωt. El ángulo que forma con la segunda barra será su complementario, π / 2 − θ. Los módulos de las dos fuerzas valen entonces
