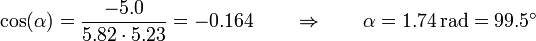Cálculo de ángulo entre dos vectores
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== ==Solución== Obtenemos el ángulo a partir del producto escalar de los dos vectores <center><math>\vec{v}\cdot\vec{a}=|\vec{v}||\vec{a}|\cos(\alpha)\qquad\Righta…') |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| + | Halle el ángulo que forman los vectores | ||
| + | |||
| + | <center><math>\vec{A}=24\vec{\imath}-32\vec{k}\qquad\mbox{y}\qquad \vec{B}=16\vec{\jmath}+12\vec{k}</math></center> | ||
| + | |||
==Solución== | ==Solución== | ||
Obtenemos el ángulo a partir del producto escalar de los dos vectores | Obtenemos el ángulo a partir del producto escalar de los dos vectores | ||
Revisión de 17:50 13 nov 2011
1 Enunciado
Halle el ángulo que forman los vectores
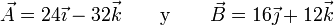
2 Solución
Obtenemos el ángulo a partir del producto escalar de los dos vectores
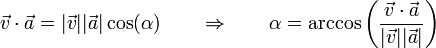
Tenemos que
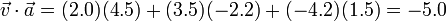
y que
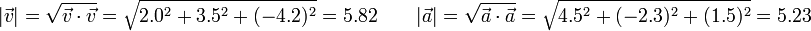
lo que nos da