Dos bloques apilados
De Laplace
| Línea 9: | Línea 9: | ||
<center>[[Archivo:dos-masas-apiladas.png]]</center> | <center>[[Archivo:dos-masas-apiladas.png]]</center> | ||
| - | == | + | ==Introducción== |
| + | ==Diagramas de cuerpo libre== | ||
Cuando tenemos un sistema formado por varias partes, la técnica de solución pasa por dibujar los diagramas de cuerpo libre, en los que cada elemento se representa por separado, indicando todas las fuerzas a que está sometido. Entre las fuerzas aplicadas se incluyen las de reacción vincular, debidas a contactos y ligaduras. | Cuando tenemos un sistema formado por varias partes, la técnica de solución pasa por dibujar los diagramas de cuerpo libre, en los que cada elemento se representa por separado, indicando todas las fuerzas a que está sometido. Entre las fuerzas aplicadas se incluyen las de reacción vincular, debidas a contactos y ligaduras. | ||
| Línea 38: | Línea 39: | ||
<center><math>m_2\vec{g}+\vec{F}_{n1\to 2}+ \vec{F}_{r1\to 2} = m_2\vec{a}_2</math></center> | <center><math>m_2\vec{g}+\vec{F}_{n1\to 2}+ \vec{F}_{r1\to 2} = m_2\vec{a}_2</math></center> | ||
| + | Por la tercera ley de Newton se cumple | ||
| + | <math>\vec{F}_{n1\to 2} = -\vec{F}_{n2\to 1}\qquad\qquad \vec{F}_{n1\to 2} = -\vec{F}_{n2\to 1}</math> | ||
| + | ==Componentes verticales== | ||
| + | ==Caso sin rozamiento con el suelo== | ||
| + | ==Caso general== | ||
| + | ==Casos prácticos== | ||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
Revisión de 12:48 12 nov 2011
Contenido |
1 Enunciado
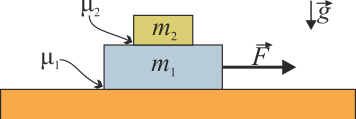
Sobre una mesa horizontal se encuentran apilados dos bloques, siendo el inferior de masa m1 y el superior de masa m2. El coeficiente de rozamiento estático del bloque inferior con la mesa vale μ1 y el del segundo bloque con el primero μ2. Los coeficientes de rozamiento dinámico valen lo mismo que los estáticos.
- Para el estado de reposo y sin fuerzas laterales aplicadas, indique la fuerza que la mesa ejerce sobre el bloque inferior y el que éste ejerce sobre el superior.
- Suponiendo μ1 = 0, se tira del bloque inferior con una fuerza horizontal F. ¿Qué fuerzas actúan sobre cada bloque? ¿Cuánto debe valer como mínimo esta fuerza si se quiere que el bloque superior se quede atrás? ¿Cuánto vale la aceleración de cada bloque para valores de la fuerza inferiores o superiores a este valor crítico?
- Resuelva las mismas cuestiones que en el apartado anterior, suponiendo ahora
.
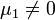- Calcule los valores de las diferentes fuerzas y las aceleraciones si
, 
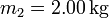, μ1 = 0.30, μ2 = 0.50 para (a) 
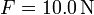(b) 
(c)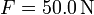 
2 Introducción
3 Diagramas de cuerpo libre
Cuando tenemos un sistema formado por varias partes, la técnica de solución pasa por dibujar los diagramas de cuerpo libre, en los que cada elemento se representa por separado, indicando todas las fuerzas a que está sometido. Entre las fuerzas aplicadas se incluyen las de reacción vincular, debidas a contactos y ligaduras.
En este caso tenemos los dos bloque s que denominaremos “1” y “2”, respectivamente. Al suelo, en el que está apoyado el bloque 1, lo etiquetaremos como “0”.
Así tenemos, para el bloque 1, las siguientes fuerzas:
- Su peso,
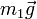causado por la atracción terrestre.
- La fuerza de reacción normal ejercida por el plano,
.
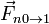- La fuerza de reacción normal debida al bloque superior,
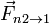. Nótese que esta fuerza no es “el peso del bloque 2” (ya que el peso de 2 es una fuerza ejercida por la tierra sobre el bloque 2. La fuerza normal de que hablamos es la fuerza elástica debida al contacto entre los dos bloques. Otra cosa es que su valor sea igual a peso de ese bloque.
- La fuerza de rozamiento debida al suelo,
.
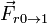- La fuerza de rozamiento debida al bloque 2,
.
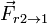De estas cinco fuerzas, las tres primeras son verticales y las dos últimas horizontales.
La suma de todas ellas nos da la aceleración de la masa 1
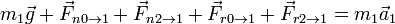
Sobre el bloque 2 actúan menos fuerzas:
- Su peso,
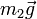causado por la atracción terrestre.
- La fuerza de reacción normal debida al bloque inferior,
.
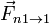- La fuerza de rozamiento debida al bloque 1,
.
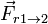que, por aplicación de la segunda ley de Newton nos da
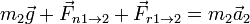
Por la tercera ley de Newton se cumple
