1.11. Vectores con tres condiciones (Ex.Nov/11)
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 24: | Línea 24: | ||
<center><math>\left|(a_x\,\vec{\imath}+a_y\,\vec{\jmath}+a_z\,\vec{k})\cdot(\vec{\imath}\wedge\vec{k})\right|=|a_y|=6</math></center> | <center><math>\left|(a_x\,\vec{\imath}+a_y\,\vec{\jmath}+a_z\,\vec{k})\cdot(\vec{\imath}\wedge\vec{k})\right|=|a_y|=6</math></center> | ||
| - | + | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | ||
Revisión de 20:37 9 nov 2011
1 Enunciado
Determine todos los vectores libres que cumplen las tres siguientes condiciones:
1) Tener una longitud de 14 m.
2) Ser ortogonal al vector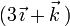 
m.
3) Formar junto a los vectores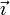 
m y
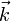m un paralelepípedo de volumen igual a 6 m3.
2 Solución
Exigiremos a un vector genérico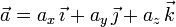 
las tres condiciones dadas. Por comodidad, prescindiremos de las unidades hasta llegar a la solución final (son todas unidades del SI).
La longitud de un vector es su módulo. Así que el cuadrado del módulo de 
debe ser:
La condición de ortogonalidad entre dos vectores viene dada por la nulidad de su producto escalar:
El volumen del paralelepípedo que tiene a tres vectores por aristas es igual al valor absoluto de su producto mixto:
