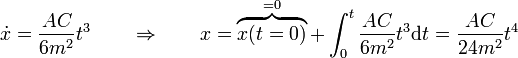Movimiento a partir de una fuerza conocida

De Laplace

(Diferencias entre revisiones)

Revisión de 23:36 8 nov 2011

1 Enunciado

Una partícula material de masa $m$ parte del origen de coordenadas con velocidad 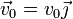$\vec{v}_0=v_0\vec{\jmath}$ , encontrándose sometida en todo momento a la fuerza dependiente de la posición

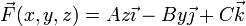
$\vec{F}(x,y,z)=Az\vec{\imath}-By\vec{\jmath}+C\vec{k}$

siendo 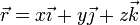$\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$ la posición instantánea de la partícula, y $A$ , $B$ y $C$ constantes positivas conocidas.

Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, $t$ .

2 Solución

La segunda ley de Newton nos permite calcular la aceleración de la partícula para cada punto

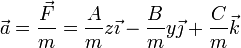
$\vec{a}=\frac{\vec{F}}{m}=\frac{A}{m}z\vec{\imath}-\frac{B}{m}y\vec{\jmath}+\frac{C}{m}\vec{k}$

La primera tentación, para hallar la posición en cada instante, es integrar dos veces

$\vec{v}=\vec{v}_0+\int_0^t \vec{a}\,\mathrm{d}t\qquad\qquad\vec{r}=\vec{r}_0+\int_0^t \vec{v}\,\mathrm{d}t$

Sin embargo, aunque estas fórmulas son correctas, no nos sirven de nada, ya que no conocemos la aceleración como función del tiempo, sino de la posición, que es lo que deseamos hallar.

Debemos, por fuerza resolver la ecuación diferencial.

Un primer paso que nos puede ayudar a abordar el problema consiste en separar por componentes.

La aceleración, por definición, es la segunda derivada de la posición respecto al tiempo

$\vec{a}=\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t}=\ddot{x}\vec{\imath}+\ddot{y}\vec{\jmath}+\ddot{z}\vec{k}$

Igualando componente a componente nos queda el sistema de ecuaciones diferenciales

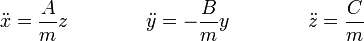
$\ddot{x}=\frac{A}{m}z\qquad\qquad \ddot{y}=-\frac{B}{m}y\qquad\qquad \ddot{z}=\frac{C}{m}$

Junto con las condiciones iniciales para la posición

$\vec{r}(t=0) = \vec{0} \qquad\Rightarrow\qquad \left\{\begin{array}{l}x(t=0)=0\\ y(t=0)=0\\ z(t=0)=0\end{array}\right.$

y la velocidad

$\vec{v}(t=0) = v_0\vec{\jmath} \qquad\Rightarrow\qquad \left\{\begin{array}{l}\dot{x}(t=0)=0\\ \dot{y}(t=0)=v_0\\ \dot{z}(t=0)=0\end{array}\right.$

La tentación, de nuevo, es calcular $x (t)$ por una doble integración. Pero tampoco podemos hacerlo. Para integrar necesitamos conocer $z (t)$ , que aun no tenemos.

Componente z: ¿Podemos hallar $z (t)$ independientemente? Pues sí, ya que la ecuación de movimiento nos dice que la segunda derivada es una constante, lo que se puede integrar de forma inmediata para hallar la velocidad

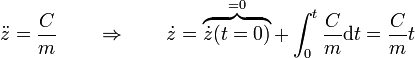
$\ddot{z}=\frac{C}{m}\qquad\Rightarrow\qquad \dot{z}=\overbrace{\dot{z}(t=0)}^{=0}+\int_0^t \frac{C}{m}\mathrm{d}t = \frac{C}{m}t$

y de aquí la coordenada

z

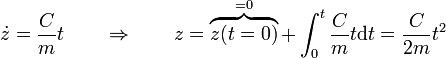
$\dot{z}=\frac{C}{m}t\qquad\Rightarrow\qquad z=\overbrace{z(t=0)}^{=0}+\int_0^t \frac{C}{m}t\mathrm{d}t = \frac{C}{2m}t^2$

Componente x: Una que conocemos $z (t)$ ya sí podemos sustituir en la ecuación para $x$ e integrar una primera vez

$\ddot{x}=\frac{A}{m}z=\frac{AC}{2m}t^2\qquad\Rightarrow\qquad \dot{x}=\overbrace{\dot{x}(t=0)}^{=0}+\int_0^t \frac{AC}{2m^2}t^2\mathrm{d}t = \frac{AC}{6m}t^3$

y una segunda

$\dot{x}=\frac{AC}{6m^2}t^3\qquad\Rightarrow\qquad x=\overbrace{x(t=0)}^{=0}+\int_0^t \frac{AC}{6m^2}t^3\mathrm{d}t = \frac{AC}{24m^2}t^4$

@@ Línea 38: / Línea 38: @@
 <center><math>\vec{v}(t=0) = v_0\vec{\jmath} \qquad\Rightarrow\qquad \left\{\begin{array}{l}\dot{x}(t=0)=0\\ \dot{y}(t=0)=v_0\\ \dot{z}(t=0)=0\end{array}\right.</math></center>
+La tentación, de nuevo, es calcular <math>x(t)</math> por una doble integración. Pero tampoco podemos hacerlo. Para integrar necesitamos conocer <math>z(t)</math>, que aun no tenemos.
+;Componente z: ¿Podemos hallar <math>z(t)</math> independientemente? Pues sí, ya que la ecuación de movimiento nos dice que la segunda derivada es una constante, lo que se puede integrar de forma inmediata para hallar la velocidad
+<center><math>\ddot{z}=\frac{C}{m}\qquad\Rightarrow\qquad \dot{z}=\overbrace{\dot{z}(t=0)}^{=0}+\int_0^t \frac{C}{m}\mathrm{d}t = \frac{C}{m}t</math></center>
+:y de aquí la coordenada <math>z</math>
+<center><math>\dot{z}=\frac{C}{m}t\qquad\Rightarrow\qquad z=\overbrace{z(t=0)}^{=0}+\int_0^t \frac{C}{m}t\mathrm{d}t = \frac{C}{2m}t^2</math></center>
+;Componente x: Una que conocemos <math>z(t)</math> ya sí podemos sustituir en la ecuación para <math>x</math> e integrar una primera vez
+<center><math>\ddot{x}=\frac{A}{m}z=\frac{AC}{2m}t^2\qquad\Rightarrow\qquad \dot{x}=\overbrace{\dot{x}(t=0)}^{=0}+\int_0^t \frac{AC}{2m^2}t^2\mathrm{d}t = \frac{AC}{6m}t^3</math></center>
+:y una segunda
+<center><math>\dot{x}=\frac{AC}{6m^2}t^3\qquad\Rightarrow\qquad x=\overbrace{x(t=0)}^{=0}+\int_0^t \frac{AC}{6m^2}t^3\mathrm{d}t = \frac{AC}{24m^2}t^4</math></center>
 [[Categoría:Problemas de dinámica de la partícula (GIE)]]

Movimiento a partir de una fuerza conocida

De Laplace

Revisión de 23:36 8 nov 2011

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES