Pequeña espira junto a hilo

De Laplace

Revisión de 09:43 15 jul 2008 (ver código fuente) Antonio (Discusión | contribuciones) (→Campo magnético debido al hilo) ← Edición más antigua		Revisión de 09:51 15 jul 2008 (ver código fuente) Antonio (Discusión | contribuciones) (→Campo magnético debido al hilo) Edición más nueva →
Línea 8:		Línea 8:
	==Solución==		==Solución==
	===Campo magnético debido al hilo===		===Campo magnético debido al hilo===
		+	Consideremos primero el hilo infinito, colineal con el eje <math>OZ</math>, para calcular el campo de inducción magnética <math>\mathbf{B}(\mathbf{r})</math> creado cuando por él circula una corriente eléctrica de intensidad <math>I_0</math>. Para ello podemos seguir dos procedimientos distintos:
		+
	====Por integración directa====		====Por integración directa====
		+	Llamemos $\Lambda$ a nuestro conductor filiforme rectilíneo que se extiende hasta el infinito; es decir, hasta puntos suficientemente alejados de donde evaluaremos el campo. Y asumiendo que el conductor forma un circuito cerrado en el infinito, el cuál es recorrido por una intensidad de corriente $I_0$, se puede aplicar la ley de Biot y Savart para calcular el campo $\mathbf{B}(\mathbf{r})$ creado por dicha corriente:
		+
		+	<center><math>\mathbf{B}(\mathbf{r})=\frac{\mu_0\ I_0}{4\pi}\ \int_\Lambda\!\frac{\mathrm{d}\mathbf{r'}\times\big(\mathbf{r}-\mathbf{r}'\big)}{|\mathbf{r}-\mathbf{r'}|^3}</math></center>
		+
		+	donde <math>I_0 \mathrm{d}\mathbf{r'}\rfloor_\Lambda=I_0\mathrm{d}z'\mathbf{u}_z</math> es el elemento de corriente en un punto <math>P'</math> del hilo, cuya posición viene dada por <math>\mathbf{r'}=z'\mathbf{u}_z</math>. El radiovector <math>\mathbf{r}=\rho\mathbf{u}_{\rho}(\varphi)+z\mathbf{u}_z</math> describe la posición del punto arbitrario <math>P</math> donde se evalúa el campo. Operando con estas expresiones en la ecuación anterior se obtiene:
		+
		+	<center><math>\mathbf{B}(\mathbf{r})=\mathbf{u}_\varphi(\varphi)\ \frac{\mu_0\ I_0}{4\pi}\int_{-\infty}^\infty\!\frac{\rho\ \mathrm{d}z'}{\big[\rho^2+(z-z')^2\big]^{3/2}}</math></center>
		+
		+	Obsérvese que el vector unitario <math>\mathbf{u}_\varphi</math> sale fuera de la integral ya que sólo depende de la variable <math>\varphi</math>, que es una de las coordenadas del punto <math>P(\rho,\varphi,z)</math> donde se evalúa el campo y, por tanto, independiente de la variable de integración <math>z'</math>.
		+
		+	La integral que aparece en al expresión anterior puede integrarse  fácilmente mediante un sencillo cambio de variable, obteniéndose así el campo de inducción magnética creado por una corriente rectilínea de longitud indefinida:
		+
		+
		+	<math>\left.\begin{array}{l}
		+	\displaystyle \frac{z-z'}{\rho}=\tan\alpha\\ \\
		+	\mathrm{d}z'=-\frac{\rho}{\cos^2\alpha}\mathrm{d}\alpha
		+	\end{array}\right\}</math>\quad \entonces \quad\mathbf{B}(\mathbf{r})=-\mathbf{u}_\varphi(\varphi)\
		+	\frac{\mu_0\ I_0}{4
		+	\pi\rho}\int_{\pi/2}^{-\pi/2}\!\!\cos\alpha \mathrm{d}\alpha\quad \rightarrow
		+	\quad \fbox{$\displaystyle\mathbf{B}(\mathbf{r})=
		+	\frac{\mu_0\ I_0}{2
		+	\pi\rho}\mathbf{u}_\varphi(\varphi)$}
		+
		+
	====Por aplicación de la Ley de Ampère====		====Por aplicación de la Ley de Ampère====

---

Revisión de 09:51 15 jul 2008

Contenido 1 Enunciado 2 Solución 2.1 Campo magnético debido al hilo 2.1.1 Por integración directa 2.1.2 Por aplicación de la Ley de Ampère 2.2 Fuerza sobre la espira 2.3 Caso de una espira en movimiento

1 Enunciado

Un conductor cilíndrico de radio muy pequeño a y longitud indefinida es recorrido por una corriente continua I₀. Una espira cuadrada muy pequeña, de lado b, resistencia R y autoinducción despreciable, es coplanaria con el hilo y se encuentra situada a una distancia y de éste ().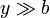

1. Calcule, detallando los pasos, el campo magnético producido por el hilo en su exterior
2. Si por la espira circula una corriente I₁, ¿qué fuerza ejerce el hilo sobre ella?
3. Suponga que la espira se aleja del hilo, sin cambiar su orientación, de modo que y = y₀ + v₀t, ¿cuánto vale la corriente I₁ inducida en la espira en un instante t? ¿Y la fuerza que el hilo ejerce sobre ella?

2 Solución

2.1 Campo magnético debido al hilo

Consideremos primero el hilo infinito, colineal con el eje OZ, para calcular el campo de inducción magnética 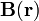creado cuando por él circula una corriente eléctrica de intensidad I₀. Para ello podemos seguir dos procedimientos distintos:

2.1.1 Por integración directa

Llamemos $\Lambda$ a nuestro conductor filiforme rectilíneo que se extiende hasta el infinito; es decir, hasta puntos suficientemente alejados de donde evaluaremos el campo. Y asumiendo que el conductor forma un circuito cerrado en el infinito, el cuál es recorrido por una intensidad de corriente $I_0$, se puede aplicar la ley de Biot y Savart para calcular el campo $\mathbf{B}(\mathbf{r})$ creado por dicha corriente:

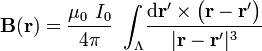
donde 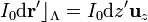es el elemento de corriente en un punto P' del hilo, cuya posición viene dada por 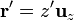. El radiovector 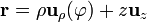describe la posición del punto arbitrario P donde se evalúa el campo. Operando con estas expresiones en la ecuación anterior se obtiene:

Obsérvese que el vector unitario 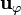sale fuera de la integral ya que sólo depende de la variable , que es una de las coordenadas del punto donde se evalúa el campo y, por tanto, independiente de la variable de integración z'.

La integral que aparece en al expresión anterior puede integrarse fácilmente mediante un sencillo cambio de variable, obteniéndose así el campo de inducción magnética creado por una corriente rectilínea de longitud indefinida:

\quad \entonces \quad\mathbf{B}(\mathbf{r})=-\mathbf{u}_\varphi(\varphi)\ \frac{\mu_0\ I_0}{4 \pi\rho}\int_{\pi/2}^{-\pi/2}\!\!\cos\alpha \mathrm{d}\alpha\quad \rightarrow \quad \fbox{$\displaystyle\mathbf{B}(\mathbf{r})= \frac{\mu_0\ I_0}{2 \pi\rho}\mathbf{u}_\varphi(\varphi)$}

2.1.2 Por aplicación de la Ley de Ampère

2.2 Fuerza sobre la espira

2.3 Caso de una espira en movimiento