Entrar Página Discusión Historial Go to the site toolbox

Evolvente de una circunferencia (GIE)

De Laplace

(Diferencias entre revisiones)
(→Vector de posición)
(→Vector de posición)
Línea 52: Línea 52:
y que
y que
-
<center><math>\frac{\mathrm{d}\vec{u}_2}{\mathrm{d}t}=\omega\cos(\omega t)\vec{\imath}+\omega\,\mathrm{sen}(\omega t)\vec{\jmath}=-\omega \vec{u}_1</math></center>
+
<center><math>\frac{\mathrm{d}\vec{u}_2}{\mathrm{d}t}=\omega\cos(\omega t)\vec{\imath}+\omega\,\mathrm{sen}(\omega t)\vec{\jmath}=\omega \vec{u}_1</math></center>
==Velocidad y aceleración==
==Velocidad y aceleración==

Revisión de 09:38 2 nov 2011

Contenido

1 Enunciado

La evolvente de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio A que se va desenrollando a ritmo constante, de forma que el punto C donde el hilo deja de hacer contacto con el carrete forma un ángulo θ = ωt con el eje OX. Una partícula material se encuentra en el punto P situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.

  1. Determine el vector de posición de la partícula.
  2. Calcule la velocidad y la aceleración de la partícula.
  3. Determine la distancia recorrida por la partícula como función del tiempo, s = s(t).
  4. Halle los vectores tangente y normal a la trayectoria.
  5. Halle el radio de curvatura y el centro de curvatura.

2 Vector de posición

Por adición de vectores

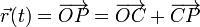
\vec{r}(t) = \overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{CP}

El vector \overrightarrow{OC} es radial y forma un ángulo ωt con el eje OX. Su módulo es A, el radio del carrete:

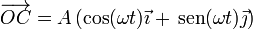
\overrightarrow{OC}=A\left(\cos(\omega t)\vec{\imath}+\,\mathrm{sen}(\omega t)\vec{\jmath}\right)

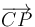El vector \overrightarrow{CP} es tangente a la circunferencia y por tanto perpendicular al radio. Obtenemos el unitario en esta dirección intercambiando las dos componentes del unitario radial y cambiándole el signo a una de ellas. El sentido lo da el que para ωt < π / 2 la componente X es positiva y la Y es negativa, por tanto

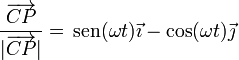
\frac{\overrightarrow{CP}}{|\overrightarrow{CP}|} = \,\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath}

El módulo de 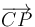\overrightarrow{CP} lo da la cantidad de hilo desenrollado hasta ese momento, igual al producto del radio por el ángulo, L = Aωt

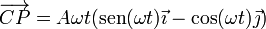
\overrightarrow{CP}= A\omega t(\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath})

Sumando los dos vectores obtenemos el vector de posición

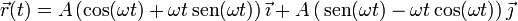
\vec{r}(t) = A\left(\cos(\omega t)+\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\left(\,\mathrm{sen}(\omega t)-\omega t\cos(\omega t)\right)\vec{\jmath}

Para simplificar esta expresión, podemos ayudarnos de dos vectores unitarios auxiliares

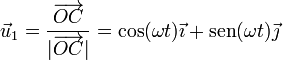
\vec{u}_1 = \frac{\overrightarrow{OC}}{|\overrightarrow{OC}|} = \cos(\omega t)\vec{\imath}+\mathrm{sen}(\omega t)\vec{\jmath}        \vec{u}_2 = \frac{\overrightarrow{CP}}{|\overrightarrow{CP}|} = \,\mathrm{sen}(\omega t)\vec{\imath}-\cos(\omega t)\vec{\jmath}

Estos dos vectores son unitarios y ortogonales

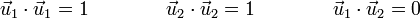
\vec{u}_1\cdot\vec{u}_1 = 1\qquad\qquad \vec{u}_2\cdot\vec{u}_2 = 1\qquad\qquad\vec{u}_1\cdot\vec{u}_2 = 0

y por tanto constituyen una base (en el plano). Empleando estos dos vectores, la posición instantánea se escribe

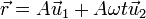
\vec{r}=A\vec{u}_1 + A\omega t\vec{u}_2

Los vectores 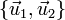\{\vec{u}_1,\vec{u}_2\} son dependientes del tiempo, y por tanto, a la hora de derivar o integrar, habrá que tenerlos en cuenta. Se cumple que

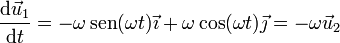
\frac{\mathrm{d}\vec{u}_1}{\mathrm{d}t}=-\omega\,\mathrm{sen}(\omega t)\vec{\imath}+\omega\cos(\omega t)\vec{\jmath}=-\omega \vec{u}_2

y que

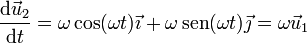
\frac{\mathrm{d}\vec{u}_2}{\mathrm{d}t}=\omega\cos(\omega t)\vec{\imath}+\omega\,\mathrm{sen}(\omega t)\vec{\jmath}=\omega \vec{u}_1

3 Velocidad y aceleración

3.1 Velocidad

Derivando el vector de posición respecto al tiempo obtenemos

\vec{v}(t)=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=A\omega^2 t\cos(\omega t)\vec{\imath}+A\omega^2t\,\mathrm{sen}(\omega t)\vec{\jmath}

3.2 Aceleración

Derivando de nuevo

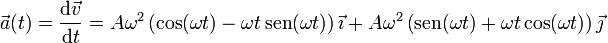
\vec{a}(t) =\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=A\omega^2\left(\cos(\omega t)-\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\omega^2\left(\mathrm{sen}(\omega t)+\omega t\cos(\omega t)\right)\vec{\jmath}
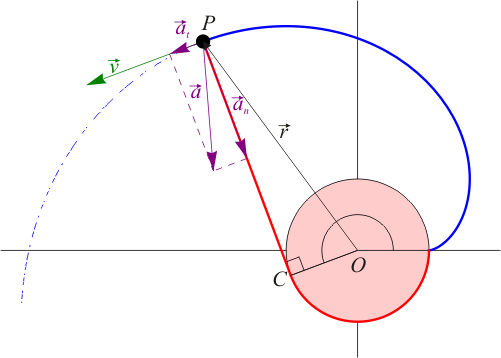
Archivo:esquema-evolvente.png

4 Distancia recorrida

La rapidez con que se recorre la curva la da el módulo de la velocidad

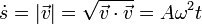
\dot{s}=|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}} = A\omega^2 t

e integrando esta ecuación obtenemos la distancia recorrida como función del tiempo

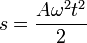
s = \frac{A\omega^2t^2}{2}

5 Vectores tangente y normal

5.1 Vector tangente

Hallamos el vector unitario tangente normalizando la velocidad

\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\cos(\omega t)\vec{\imath}+\mathrm{sen}(\omega t)\vec{\jmath}

Obsérvese que el vector unitario tangente resulta paralelo al vector \overrightarrow{OC}

5.2 Vector normal

La aceleración tangencial de la partícula la podemos hallar derivando la rapidez

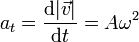
a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t} = A\omega^2

y en forma vectorial

\vec{a}_t = a_t\vec{T}= A\omega^2\cos(\omega t)\vec{\imath}+A\omega^2\mathrm{sen}(\omega t)\vec{\jmath}

Hallamos la aceleración normal restando la tangencial de la completa

\vec{a}_n = \vec{a}-\vec{a}_t = \left(A\omega^2\left(\cos(\omega t)-\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\omega^2\left(\mathrm{sen}(\omega t)+\omega t\cos(\omega t)\right)\vec{\jmath}\right)-\left(A\omega^2\cos(\omega t)\vec{\imath}+A\omega^2\mathrm{sen}(\omega t)\vec{\jmath}\right)

lo que nos da

\vec{a}_n= -A\omega^3\,\mathrm{sen}(\omega t)\vec{\imath}+A\omega^3 t\cos(\omega t)\vec{\jmath}

Este vector tiene por módulo

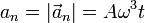
a_n = |\vec{a}_n| = A\omega^3 t

Dividiendo el vector aceleración normal por su módulo obtenemos el vector normal

\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}

6 Radio y centro de curvatura

Podemos hallar el centro y el radio de curvatura directamente a partir de la velocidad y la aceleración. Sin embargo, es más ilustrativo emplear componentes intrínsecas de la aceleración

Una vez que tenemos el vector tangente y el vector normal, podemos, por simple inspección, escribir

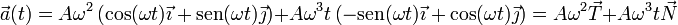
\vec{a}(t) =A\omega^2\left(\cos(\omega t)\vec{\imath}+\mathrm{sen}(\omega t)\vec{\jmath}\right)+A\omega^3t\left(-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\right) = A\omega^2\vec{T}+A\omega^3t\vec{N}

y por tanto

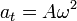
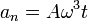
a_t = A\omega^2\,        a_n=A\omega^3t\,

Vemos que, dado que la aceleración tangencial es constante, el movimiento es uniformemente acelerado.

El radio de curvatura lo obtenemos de la velocidad y la aceleración normal

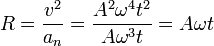
R = \frac{v^2}{a_n}=\frac{A^2\omega^4t^2}{A\omega^3t}=A\omega t

Vemos que va aumentando gradualmente en el tiempo, como corresponde a que la curva es una espiral que se va abriendo.

La posición de los centros de curvatura es

\vec{r}_c=\vec{r}+R\vec{N} = A\left(\cos(\omega t)+\omega t\,\mathrm{sen}(\omega t)\right)\vec{\imath}+A\left(\,\mathrm{sen}(\omega t)-\omega t\cos(\omega t)\right)\vec{\jmath}+A\omega t\left(-\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\right)

que nos da

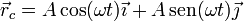
\vec{r}_c=A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}(\omega t)\vec{\jmath}

Pero esta es justamente la posición del punto C. Por tanto, el conjunto de los centros de curvatura (lo que se conoce como evoluta) es la propia circunferencia del carrete.

Obtenido de "http://tesla.us.es/wiki/index.php/Evolvente_de_una_circunferencia_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace