Entrar Página Discusión Historial Go to the site toolbox

3.8. Movimiento bajo fuerza central en polares

De Laplace

(Diferencias entre revisiones)
(→Conservación de la velocidad areolar)
(→Conservación de la velocidad areolar)
Línea 25: Línea 25:
<center><math>\frac{\mathrm{d}V_A}{\mathrm{d}t}=\frac{1}{2}\,\frac{\mathrm{d}(\rho^2\dot{\theta})}{\mathrm{d}t}=\frac{1}{2}\,(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta})=\frac{\rho}{2}\,(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})=\frac{\rho}{2}\,a_{\theta} </math></center>
<center><math>\frac{\mathrm{d}V_A}{\mathrm{d}t}=\frac{1}{2}\,\frac{\mathrm{d}(\rho^2\dot{\theta})}{\mathrm{d}t}=\frac{1}{2}\,(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta})=\frac{\rho}{2}\,(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})=\frac{\rho}{2}\,a_{\theta} </math></center>
-
Comprobamos, por tanto, que la conservación de la velocidad areolar como una magnitud constante a lo largo del tiempo (integral primera) se produce si y sólo si la componente acimutal de la aceleración es permanentemente nula, lo cual conlleva de forma obvia la centralidad de la fuerza respecto al origen de coordenadas:
+
Comprobamos, por tanto, que la conservación de la velocidad areolar como una magnitud constante a lo largo del tiempo se produce si y sólo si la componente acimutal de la aceleración es permanentemente nula, lo cual conlleva de forma obvia la centralidad de la fuerza respecto al origen de coordenadas:
<center><math>V_A=\mathrm{cte}\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\frac{\mathrm{d}V_A}{\mathrm{d}t}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,a_{\theta}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\vec{F}=m\vec{a}=ma_{\rho}\,\vec{u}_{\rho}=F_{\rho}\,\vec{u}_{\rho}</math></center>
<center><math>V_A=\mathrm{cte}\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\frac{\mathrm{d}V_A}{\mathrm{d}t}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,a_{\theta}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\vec{F}=m\vec{a}=ma_{\rho}\,\vec{u}_{\rho}=F_{\rho}\,\vec{u}_{\rho}</math></center>
 +
 +
Obsérvese que la conservación de la velocidad areolar está intímamente ligada a la conservación del momento cinético (respecto al mismo punto <math>O\,</math>), ya que
 +
 +
<center><math>\vec{L}_O=\vec{r}\times m\vec{v}=2m\vec{V}_A</math></center>
 +
 +
siendo la propiedad de paralelismo <math>\vec{F}\parallel\vec{r}</math> propia de las fuerzas centrales en <math>O\,</math> la que provoca que tanto la el momento cinético como la velocidad areolar respecto a <math>O\,</math> sean constantes.
==Ecuaciones horarias==
==Ecuaciones horarias==

Revisión de 11:55 27 oct 2011

Contenido

1 Enunciado

Sea una partícula P de masa m cuyo movimiento en el plano OXY se describe mediante coordenadas polares.

  1. Deduzca la expresión de su velocidad areolar respecto al origen de coordenadas O, y compruebe que la misma es constante en el tiempo si y sólo si el movimiento transcurre bajo la acción de una fuerza central en O.
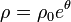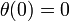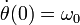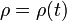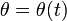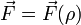  2. Sabiendo que la partícula recorre la espiral \rho=\rho_{0}e^{\theta}\, sometida a una fuerza central en O y con condiciones iniciales \theta(0)=0\, y \dot{\theta}(0)=\omega_0, determine las ecuaciones horarias \rho = \rho(t)\, y \theta = \theta(t)\,, así como el valor de dicha fuerza en función de la coordenada radial \vec{F} = \vec{F}(\rho).

2 Expresión general de la velocidad areolar

Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula

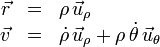
\begin{array}{rcl} \vec{r} & = & \rho\,\vec{u}_{\rho} \\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta}\end{array}

en la definición de la velocidad areolar de la partícula respecto al origen de coordenadas O\,, se obtiene

\vec{V}_A=\frac{1}{2}\,\vec{r}\times\vec{v}=\frac{1}{2}\,\rho\,\vec{u}_{\rho}\times(\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta})=\frac{1}{2}\,\rho^2\dot{\theta}\,\vec{k}

3 Conservación de la velocidad areolar

Teniendo en cuenta que la dirección del vector velocidad areolar es constante (dirección perpendicular al plano del movimiento), es evidente que la citada magnitud vectorial se conservará constante en el tiempo si y sólo si es constante la velocidad areolar escalar VA

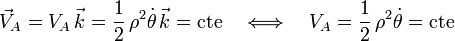
\vec{V}_A=V_A\,\vec{k}=\frac{1}{2}\,\rho^2\dot{\theta}\,\vec{k}=\mathrm{cte}\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,V_A=\frac{1}{2}\,\rho^2\dot{\theta}=\mathrm{cte}

Ahora bien, derivando respecto al tiempo VA se obtiene

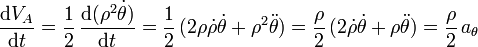
\frac{\mathrm{d}V_A}{\mathrm{d}t}=\frac{1}{2}\,\frac{\mathrm{d}(\rho^2\dot{\theta})}{\mathrm{d}t}=\frac{1}{2}\,(2\rho\dot{\rho}\dot{\theta}+\rho^2\ddot{\theta})=\frac{\rho}{2}\,(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})=\frac{\rho}{2}\,a_{\theta}

Comprobamos, por tanto, que la conservación de la velocidad areolar como una magnitud constante a lo largo del tiempo se produce si y sólo si la componente acimutal de la aceleración es permanentemente nula, lo cual conlleva de forma obvia la centralidad de la fuerza respecto al origen de coordenadas:

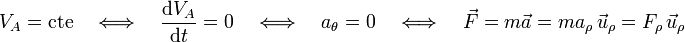
V_A=\mathrm{cte}\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\frac{\mathrm{d}V_A}{\mathrm{d}t}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,a_{\theta}=0\,\,\,\,\,\,\Longleftrightarrow\,\,\,\,\,\,\vec{F}=m\vec{a}=ma_{\rho}\,\vec{u}_{\rho}=F_{\rho}\,\vec{u}_{\rho}

Obsérvese que la conservación de la velocidad areolar está intímamente ligada a la conservación del momento cinético (respecto al mismo punto O\,), ya que

\vec{L}_O=\vec{r}\times m\vec{v}=2m\vec{V}_A

siendo la propiedad de paralelismo 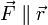\vec{F}\parallel\vec{r} propia de las fuerzas centrales en O\, la que provoca que tanto la el momento cinético como la velocidad areolar respecto a O\, sean constantes.

4 Ecuaciones horarias

5 Fuerza en función de la coordenada radial

Obtenido de "http://tesla.us.es/wiki/index.php/3.8._Movimiento_bajo_fuerza_central_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace