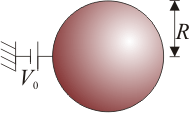
Entrar Página Discusión Historial Go to the site toolbox

Capacidad de una esfera

De Laplace

(Diferencias entre revisiones)
(→Por aplicación de la ley de Gauss)
(→Por aplicación de la ley de Gauss)
Línea 78: Línea 78:
====Por aplicación de la ley de Gauss====
====Por aplicación de la ley de Gauss====
-
[[Imagen:1esferaconductoragauss.gif|left]]Conocemos el campo en el exterior de la esfera. Si calculamos el flujo de este campo a través de una superficie cualquiera que la envuelva, el resultado es proporcional a la carga encerrada
+
[[Imagen:1esferaconductoragauss.gif|right]]Conocemos el campo en el exterior de la esfera. Si calculamos el flujo de este campo a través de una superficie cualquiera que la envuelva, el resultado es proporcional a la carga encerrada
<center><math>Q = \varepsilon_0 \oint\mathbf{E}\cdot\mathrm{d}\mathbf{S}  = \varepsilon_0\oint \frac{V_0R}{r^2}\mathbf{u}_r\cdot\mathrm{d}\mathbf{S}</math></center>
<center><math>Q = \varepsilon_0 \oint\mathbf{E}\cdot\mathrm{d}\mathbf{S}  = \varepsilon_0\oint \frac{V_0R}{r^2}\mathbf{u}_r\cdot\mathrm{d}\mathbf{S}</math></center>
Línea 85: Línea 85:
<center><math>\mathrm{d}\mathbf{S} = \mathrm{d}S\mathbf{u}_e</math>{{qquad}}<math>Q = \varepsilon_0\oint_r \frac{V_0R}{r^2}\mathrm{d}S = \frac{\varepsilon_0V_0R(4\pi r^2)}{r^2}=4\pi\varepsilon_0 R V_0</math></center>
<center><math>\mathrm{d}\mathbf{S} = \mathrm{d}S\mathbf{u}_e</math>{{qquad}}<math>Q = \varepsilon_0\oint_r \frac{V_0R}{r^2}\mathrm{d}S = \frac{\varepsilon_0V_0R(4\pi r^2)}{r^2}=4\pi\varepsilon_0 R V_0</math></center>
 +
 +
Obsérvese que el flujo es independiente del radio r de la superficie gaussiana considerada. Esto debe ser así pues la carga depositada en la esfera será la que sea, pero sin duda no va a depender de que la envolvamos con una &ldquo;bolsa&rdquo; mayor o menor.
====A partir de la densidad de carga almacenada====
====A partir de la densidad de carga almacenada====

Revisión de 16:17 14 jul 2008

Contenido

1 Enunciado

Una esfera metálica de radio a se encuentra a potencial V0 respecto al infinito. No hay más conductores en el sistema. Determine el potencial y el campo eléctrico en todos los puntos del espacio, así como la carga almacenada en la esfera conductora.

2 Solución

2.1 Potencial eléctrico

Este es el problema más sencillo que se puede plantear en problemas de campo eléctrico en presencia de conductores, ya que, como veremos, depende de una sola variable y no requiere hacer aproximación alguna.

La esfera se encuentra conectada a un generador que la sitúa a un cierto potencial eléctrico. Para conseguir esto, el generador coloca cargas en la esfera, las cuales se dispondrán en la superficie de ésta. Estas cargas provocan un campo eléctrico en el exterior. En el interior, en cambio, el potencial será constante y el campo eléctrico nulo.

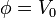
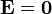
\phi = V_0\,    \mathbf{E}=\mathbf{0}\,    (r<R)\,

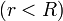
Para hallar el campo eléctrico exterior, debemos resolver la ecuación de Poisson, pero, dado que no hay más carga en el exterior, ésta se reduce a la ecuación de Laplace

\nabla^2\phi=0    (r>R)\,

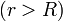
con las condiciones de contorno de que en la superficie de la esfera el potencial está fijado

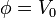
\phi = V_0\,    (r=R)\,

y de que en el infinito, que tomamos como origen de potencial, el potencial se anula

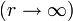
\phi \to 0\,    (r\to\infty)\,

La geometría del sistema sugiere el uso de coordenadas esféricas, en las cuales la ecuación de Laplace se escribe

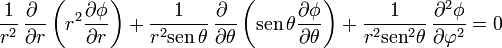
\frac{1}{r^2}\,\frac{\partial\ }{\partial r}\left(r^2\frac{\partial\phi}{\partial r}\right) + \frac{1}{r^2\operatorname{sen}\,\theta}\,\frac{\partial\ }{\partial \theta}\left(\operatorname{sen}\,\theta\frac{\partial\phi}{\partial \theta}\right) + \frac{1}{r^2\operatorname{sen}^2\theta}\,\frac{\partial^2\phi}{\partial \varphi^2}=0

Dada la simetría del sistema, en el cual las condiciones de contorno se dan en superficies r = cte podemos suponer que el potencial depende exclusivamente de la coordenada radial r. De acuerdo con el teorema de unicidad, si con esta hipótesis hallamos una solución que verifica tanto la ecuación como las condiciones de contorno, hemos resuelto el problema.

Si el potencial solo depende de r, la ecuación de Laplace se reduce a

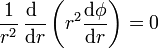
\frac{1}{r^2}\,\frac{\mathrm{d}\ }{\mathrm{d}r}\left(r^2\frac{\mathrm{d}\phi}{\mathrm{d} r}\right) =0

Integrando dos veces esta ecuación resulta un potencial de la forma

\phi = A + \frac{B}{r}

Puesto que debe anularse en el infinito, la constante A debe valer cero

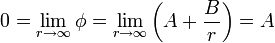
0 = \lim_{r\to\infty}\phi = \lim_{r\to\infty}\left(A+\frac{B}{r}\right) = A

y la constante B se obtiene del valor del potencial en la superficie de la esfera

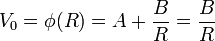
V_0 = \phi(R) = A + \frac{B}{R} = \frac{B}{R}   \Rightarrow   B=V_0R\,

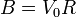
con lo que el potencial exterior vale

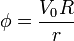
\phi = \frac{V_0R}{r}

Este potencial verifica la ecuación de Laplace y las condiciones de contorno. Es, por tanto, la solución del problema. Incluyendo la solución interior nos queda

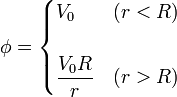
\phi = \begin{cases}V_0 & (r < R) \\ & \\ \displaystyle\frac{V_0R}{r} & (r>R)\end{cases}

Según este resultado el potencial interior es constante, mientras que el exterior equivale al de una carga puntual situada en el centro de la esfera. Esto no quiere decir que dicha carga exista (ya que quien crea el potencial son las cargas de la superficie conductora), sino que el potencial verifica que

  • No depende más que de la coordenada radial.
  • Decae como 1/r.

Podemos calcular el valor de la carga equivalente igualando la fórmula del potencial a la expresión del de una carga puntual

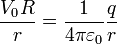
\frac{V_0R}{r} = \frac{1}{4\pi\varepsilon_0}\frac{q}{r}   \Rightarrow   q = 4\pi\varepsilon_0 R

2.2 Campo eléctrico

Una vez que tenemos el potencial, el cálculo del campo eléctrico es inmediato:

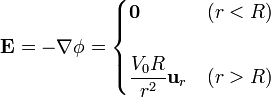
\mathbf{E} = -\nabla\phi =\begin{cases}\mathbf{0} & (r < R) \\ & \\ \displaystyle\frac{V_0R}{r^2}\mathbf{u}_r & (r>R)\end{cases}

El campo interior es nulo, como corresponde a un conductor en equilibrio electrostático.

Nótese que se obtendría el mismo resultado si en lugar de una esfera maciza tuviéramos una superficie conductora.

2.3 Carga almacenada

La carga almacenada en la superficie de la esfera podemos obtenerla por varios métodos equivalentes:

2.3.1 Por aplicación de la ley de Gauss

Conocemos el campo en el exterior de la esfera. Si calculamos el flujo de este campo a través de una superficie cualquiera que la envuelva, el resultado es proporcional a la carga encerrada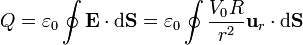
Q = \varepsilon_0 \oint\mathbf{E}\cdot\mathrm{d}\mathbf{S} = \varepsilon_0\oint \frac{V_0R}{r^2}\mathbf{u}_r\cdot\mathrm{d}\mathbf{S}

Considerando en particular una superficie esférica concéntrica con la esfera conductora

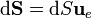
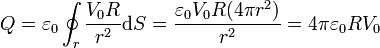
\mathrm{d}\mathbf{S} = \mathrm{d}S\mathbf{u}_e    Q = \varepsilon_0\oint_r \frac{V_0R}{r^2}\mathrm{d}S = \frac{\varepsilon_0V_0R(4\pi r^2)}{r^2}=4\pi\varepsilon_0 R V_0

Obsérvese que el flujo es independiente del radio r de la superficie gaussiana considerada. Esto debe ser así pues la carga depositada en la esfera será la que sea, pero sin duda no va a depender de que la envolvamos con una “bolsa” mayor o menor.

2.3.2 A partir de la densidad de carga almacenada

2.3.3 A partir de la expresión del potencial

Obtenido de "http://tesla.us.es/wiki/index.php/Capacidad_de_una_esfera"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace