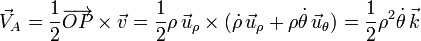Entrar Página Discusión Historial Go to the site toolbox

3.8. Movimiento bajo fuerza central en polares

De Laplace

(Diferencias entre revisiones)
(→Expresión general de la velocidad areolar)
(→Expresión general de la velocidad areolar)
Línea 9: Línea 9:
Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula
Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula
-
<center><math>\begin{array}{rcl} \vec{OP} & = & \rho\,\vec{u}_{\rho} \\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta}\end{array}</math></center>
+
<center><math>\begin{array}{rcl} \overrightarrow{OP}=\vec{r} & = & \rho\,\vec{u}_{\rho} \\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta}\end{array}</math></center>
en la definición de la velocidad areolar de la partícula respecto al punto <math>O\,</math>, se obtiene
en la definición de la velocidad areolar de la partícula respecto al punto <math>O\,</math>, se obtiene
-
<center><math>\vec{V}_A=\frac{1}{2}\vec{OP}\times\vec{v}=\frac{1}{2}\rho\,\vec{u}_{\rho}\times(\dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta})=\frac{1}{2}\rho^2\dot{\theta}\,\vec{k}</math></center>
+
<center><math>\vec{V}_A=\frac{1}{2}\overrightarrow{OP}\times\vec{v}=\frac{1}{2}\rho\,\vec{u}_{\rho}\times(\dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta})=\frac{1}{2}\rho^2\dot{\theta}\,\vec{k}</math></center>
==Conservación de la velocidad areolar==
==Conservación de la velocidad areolar==

Revisión de 20:07 26 oct 2011

Contenido

1 Enunciado

Sea una partícula P de masa m cuyo movimiento en el plano OXY se describe mediante coordenadas polares.

  1. Deduzca la expresión de su velocidad areolar respecto al origen de coordenadas O, y compruebe que la misma es constante en el tiempo si y sólo si el movimiento transcurre bajo la acción de una fuerza central en O.
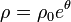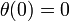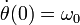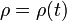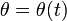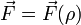  2. Sabiendo que la partícula recorre la espiral \rho=\rho_{0}e^{\theta}\, sometida a una fuerza central en O y con condiciones iniciales \theta(0)=0\, y \dot{\theta}(0)=\omega_0, determine las ecuaciones horarias \rho = \rho(t)\, y \theta = \theta(t)\,, así como el valor de dicha fuerza en función de la coordenada radial \vec{F} = \vec{F}(\rho).

2 Expresión general de la velocidad areolar

Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula

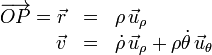
\begin{array}{rcl} \overrightarrow{OP}=\vec{r} & = & \rho\,\vec{u}_{\rho} \\ \vec{v} & = & \dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta}\end{array}

en la definición de la velocidad areolar de la partícula respecto al punto O\,, se obtiene

\vec{V}_A=\frac{1}{2}\overrightarrow{OP}\times\vec{v}=\frac{1}{2}\rho\,\vec{u}_{\rho}\times(\dot{\rho}\,\vec{u}_{\rho}+\rho\dot{\theta}\,\vec{u}_{\theta})=\frac{1}{2}\rho^2\dot{\theta}\,\vec{k}

3 Conservación de la velocidad areolar

4 Ecuaciones horarias

5 Fuerza en función de la coordenada radial

Obtenido de "http://tesla.us.es/wiki/index.php/3.8._Movimiento_bajo_fuerza_central_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace