3.12. Equilibrio de partícula en hélice
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una partícula de masa <math>m</math> se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante <math>k</math> y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada en la hélice de ecuaciones <math>x = A\,\mathrm{cos}(\theta)</math>, <math>y = A\,\mathrm{sen}(\theta)</math>, <math>z = b\theta/(2\pi)</math>. | + | Una partícula de masa <math>m</math> se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante <math>k</math> y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada en la hélice de ecuaciones <math>x = A\,\mathrm{cos}(\theta)</math>, <math>y = A\,\mathrm{sen}(\theta)</math>, <math>z = b\,\theta/(2\pi)</math>. |
# Determine la posición de equilibrio de la partícula sobre la hélice. | # Determine la posición de equilibrio de la partícula sobre la hélice. | ||
# Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio. | # Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio. | ||
| - | # Determine la energía potencial como función del parámetro <math>\theta</math> y discuta la estabilidad de la posición de equilibrio. | + | # Determine la energía potencial como función del parámetro <math>\theta\,</math> y discuta la estabilidad de la posición de equilibrio. |
[[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | [[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | ||
Revisión de 18:44 24 oct 2011
Enunciado
Una partícula de masa m se encuentra sometida simultáneamente a su peso y a la fuerza atractiva de un resorte elástico de constante k y longitud natural nula anclado en el origen de coordenadas. La partícula está ensartada en la hélice de ecuaciones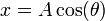 
, 
, 
.
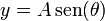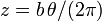- Determine la posición de equilibrio de la partícula sobre la hélice.
- Calcule la fuerza de reacción vincular que ejerce la hélice sobre la partícula en la posición de equilibrio.
- Determine la energía potencial como función del parámetro
y discuta la estabilidad de la posición de equilibrio.
