Aplicaciones de las leyes de Newton (GIE)
De Laplace
(→Movimiento con rozamiento) |
(→Oscilador armónico) |
||
| Línea 95: | Línea 95: | ||
==Oscilador armónico== | ==Oscilador armónico== | ||
| + | ===Ley de Hooke=== | ||
| + | ===Movimiento de un oscilador armónico=== | ||
| + | ====Horizontal==== | ||
| + | ====Vertical==== | ||
| + | ===Asociaciones de osciladores=== | ||
| + | ===Oscilaciones no lineales. Péndulo simple=== | ||
| + | |||
==Movimiento sobre una superficie== | ==Movimiento sobre una superficie== | ||
==Tensión de un hilo== | ==Tensión de un hilo== | ||
Revisión de 10:51 23 oct 2011
Contenido |
1 Caída de los cuerpos
En las proximidades de la superficie terrestre, la ley de Newton de la Gravitación Universal se reduce a
siendo
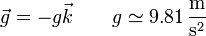
Una cantidad independiente de la masa del cuerpo.
Si suponemos que no hay otra fuerza actuando sobre la partícula, la aplicación de la segunda ley de Newton nos da
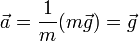
esto es que, como ya descubrió Galileo
- En ausencia de rozamiento, todos los cuerpos caen con la misma aceleración.
Esto es, la percepción cotidiana, formulada por Aristóteles, de que los cuerpos pesados caen más rápidamente que los ligeros no se debe a la diferencia en sus pesos, sino a las diferentes fuerzas de rozamiento que actúan sobre ellos.
1.1 Movimiento sin rozamiento
En ausencia de rozamiento, el movimiento de un cuerpo sometido exclusivamente a la acción de sus peso es uno parabólico, ya que la integración de las ecuaciones de movimiento es inmediata. De la aceleración
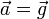
resulta la velocidad
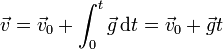
y de aquí la posición
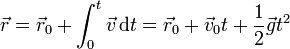
Separando en componentes quedan las ecuaciones horarias
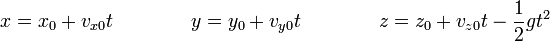
Vemos que la coordenada vertical sigue un movimiento uniformemente acelerado, mientras que las horizontales varían uniformemente.
1.2 Movimiento con rozamiento
Cuando tenemos en cuenta el rozamiento con el aire el problema se complica bastante. En el caso realista de un objeto que se mueve por el aire, la fuerza de rozamiento sería cuadrática
siendo 
la velocidad del aire que rodea a la partícula (el viento). Esto convierte la ecuación de movimiento en una ecuación diferencial
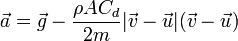
La aceleración en cada punto depende de la velocidad que tenga, por lo que no se puede simplemente integrar. Además, aparece la velocidad del aire circundante que puede ser variable en el tiempo o dependiente de la posición (hace más viento a alturas mayores). Incluso, para grandes alturas, la densidad ρ que es la del aire, también será dependiente de la posición.
Por ello, no existe una solución analítica general para este tipo de movimiento.
El caso más sencillo de este tipo de movimiento y que sí admite una solución analítica, sería el de la caída de una partícula desde una altura moderada h, partiendo del reposo, y suponiendo que no hay corrientes de aire.
En este caso, el movimiento es puramente vertical, por lo que se pueden considerar variables escalares. De esta forma la ecuación de movimiento se reduce a
Nótese que puesto que la partícula está cayendo, la fuerza de rozamiento va hacia arriba. De ahí el signo positivo que la precede.
A partir de la forma de la ecuación, podemos ver que inicialmente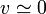 
y por tanto la aceleración es prácticamente la de la gravedad. A medida que se va acelerando aumenta la fricción, hasta que iguala al peso. A partir de ese momento la fuerza es nula y la velocidad permanece constante. Esta velocidad límite cumple
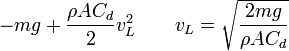
Esto nos permite escribir la ecuación de movimiento como
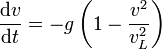
Podemos integrar esta ecuación si en vez de preguntarnos cuánto aumenta la velocidad en un instante, nos preguntamos cuánto tiempo tarda en aumentar una cierta cantidad
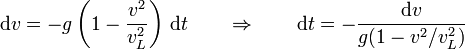
Integrando en los dos miembros
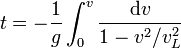
Separando en dos fracciones e integrando cada una
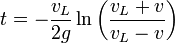
y despejando de aquí
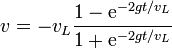
Esta función, como habíamos predicho, comienza con un crecimiento lineal, con pendiente g, para luego estabilizarse en el valor de la velocidad terminal (aunque con signo negativo, indicando que su sentido es hacia abajo).
Integrando de nuevo obtenemos la posición como función del tiempo
y resulta
