Aplicaciones de las leyes de Newton (GIE)
De Laplace
(→Movimiento sin rozamiento) |
(→Movimiento sin rozamiento) |
||
| Línea 35: | Línea 35: | ||
Separando en componentes quedan las ecuaciones horarias | Separando en componentes quedan las ecuaciones horarias | ||
| - | <center><math>x = x_0 + v_{x0]t\qquad\qquad y = y_0 + v_{y0}t\qquad\qquad z = z_0 + v_{z0 | + | <center><math>x = x_0 + v_{x0]t\qquad\qquad y = y_0 + v_{y0}t\qquad\qquad z = z_0 + v_{z0}t-\frac{1}{2}gt^2</math></center> |
Vemos que la coordenada vertical sigue un movimiento uniformemente acelerado, mientras que las horizontales varían uniformemente. | Vemos que la coordenada vertical sigue un movimiento uniformemente acelerado, mientras que las horizontales varían uniformemente. | ||
Revisión de 10:44 21 oct 2011
Contenido |
1 Caída de los cuerpos
En las proximidades de la superficie terrestre, la ley de Newton de la Gravitación Universal se reduce a
siendo
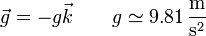
Una cantidad independiente de la masa del cuerpo.
Si suponemos que no hay otra fuerza actuando sobre la partícula, la aplicación de la segunda ley de Newton nos da
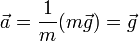
esto es que, como ya descubrió Galileo
- En ausencia de rozamiento, todos los cuerpos caen con la misma aceleración.
Esto es, la percepción cotidiana, formulada por Aristóteles, de que los cuerpos pesados caen más rápidamente que los ligeros no se debe a la diferencia en sus pesos, sino a las diferentes fuerzas de rozamiento que actúan sobre ellos.
1.1 Movimiento sin rozamiento
En ausencia de rozamiento, el movimiento de un cuerpo sometido exclusivamente a la acción de sus peso es uno parabólico, ya que la integración de las ecuaciones de movimiento es inmediata. De la aceleración
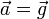
resulta la velocidad
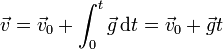
y de aquí la posición
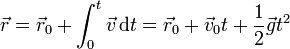
Separando en componentes quedan las ecuaciones horarias
Vemos que la coordenada vertical sigue un movimiento uniformemente acelerado, mientras que las horizontales varían uniformemente.
1.2 Movimiento con rozamiento
Cuando tenemos en cuenta el rozamiento con el aire el problema se complica bastante. En el caso realista de un objeto que se mueve por el aire, la fuerza de rozamiento sería cuadrática
siendo 
la velocidad del aire que rodea a la partícula (el viento). Esto convierte la ecuación de movimiento en una ecuación diferencial
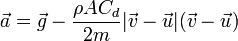
La aceleración en cada punto depende de la velocidad que tenga, por lo que no se puede simplemente integrar. Además, aparece la velocidad del aire circundante que puede ser variable en el tiempo o dependiente de la posición (hace más viento a alturas mayores). Incluso, para grandes alturas, la densidad ρ que es la del aire, también será dependiente de la posición.
Por ello, no existe una solución analítica general.
