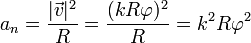Caso de movimiento circular
De Laplace
(Página creada con '==Enunciado== Una partícula describe un movimiento circular de radio <math>R</math>, tal que su velocidad angular instantánea cumple <center><math>\omega = k\varphi\,</math><…') |
|||
| Línea 13: | Línea 13: | ||
==Aceleración angular== | ==Aceleración angular== | ||
| - | ==Componentes intrínsecas== | + | Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular |
| + | |||
| + | <center><math>\alpha = \dot{\omega} = k\dot{\varphi}</math></center> | ||
| + | |||
| + | debemos escribir <math>\dot{\varphi}</math> como función del propio ángulo <math>\varphi</math>, como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular | ||
| + | |||
| + | <center><math>\dot{\varphi} = \frac{\mathrm{d}\varphi}{\mathrm{d}t} = \omega = k\varphi</math></center> | ||
| + | |||
| + | así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida | ||
| + | |||
| + | <center><math>\alpha = k^2\varphi\,</math></center> | ||
| + | |||
| + | En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro | ||
| + | |||
| + | <center><math>\vec{\alpha} = \alpha\vec{k} = k^2\varphi\vec{k}</math></center> | ||
| + | |||
| + | ==Componentes intrínsecas de la aceleración== | ||
| + | Tenemos dos componentes intrínsecas de la aceleración: | ||
| + | |||
| + | ===Aceleración tangencial=== | ||
| + | Puesto que el movimiento no es uniforme, existe una aceleración tangencial igual a la derivada temporal de la rapidez | ||
| + | |||
| + | <center><math>a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | siendo el módulo de la velocidad | ||
| + | |||
| + | <center><math>|\vec{r}| = \omega R = kR\varphi</math></center> | ||
| + | |||
| + | Derivando respecto al tiempo | ||
| + | |||
| + | <center><math>a_t = kR \dot{\varphi}= kR\omega = k^2R\varphi</math></center> | ||
| + | |||
| + | ===Aceleración normal=== | ||
| + | El valor de la aceleración normal es | ||
| + | |||
| + | <center><math>a_n = \frac{|\vec{v}|^2}{R} = \frac{(kR\varphi)^2}{R} = k^2R\varphi^2</math></center> | ||
| + | |||
==Ley horaria== | ==Ley horaria== | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
[[Categoría:Problemas del cinemática tridimensional (GIE)]] | [[Categoría:Problemas del cinemática tridimensional (GIE)]] | ||
Revisión de 19:29 12 oct 2011
Contenido |
1 Enunciado
Una partícula describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple
con k una constante y 
el ángulo que el vector de posición instantánea forma con el eje OX.
- Determine la aceleración angular de la partícula como función del ángulo .
- Halle las componentes intrínsecas de la aceleración lineal en
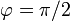y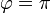 
.
- Determine la ley horaria
.
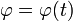2 Aceleración angular
Hallamos la aceleración angular como la derivada respecto al tiempo de la velocidad angular
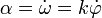
debemos escribir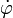 
como función del propio ángulo , como nos pide el enunciado. Esto lo hacemos simplemente observando que la derivada temporal del ángulo girado no es otra que la velocidad angular
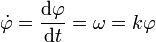
así que sustituyendo en la expresión de la aceleración angular, se obtiene la relación pedida
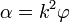
En forma vectorial, teniendo en cuenta que en un movimiento circular la aceleración angular es perpendicular al plano de giro
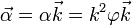
3 Componentes intrínsecas de la aceleración
Tenemos dos componentes intrínsecas de la aceleración:
3.1 Aceleración tangencial
Puesto que el movimiento no es uniforme, existe una aceleración tangencial igual a la derivada temporal de la rapidez
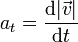
siendo el módulo de la velocidad
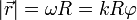
Derivando respecto al tiempo
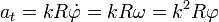
3.2 Aceleración normal
El valor de la aceleración normal es
