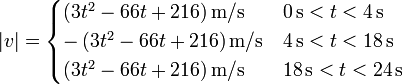Ejemplo de movimiento rectilíneo no uniforme
De Laplace
(→Máxima distancia) |
|||
| Línea 39: | Línea 39: | ||
Al final del intervalo se cumple | Al final del intervalo se cumple | ||
| - | <center><math>x(24\,\mathrm{s | + | <center><math>x(24\,\mathrm{s})=0\,\mathrm{m}</math></center> |
esto es, retorna a su posición inicial. | esto es, retorna a su posición inicial. | ||
| Línea 50: | Línea 50: | ||
<center><math>|x|_\mathrm{max}=972\,\mathrm{m}</math></center> | <center><math>|x|_\mathrm{max}=972\,\mathrm{m}</math></center> | ||
| + | |||
===Desplazamiento=== | ===Desplazamiento=== | ||
El desplazamiento es neto es la diferencia entre la posición final y la inicial | El desplazamiento es neto es la diferencia entre la posición final y la inicial | ||
Revisión de 12:52 12 oct 2011
Contenido |
1 Enunciado
Una partícula se mueve a lo largo de una recta de forma que su posición sigue la ley, en el SI
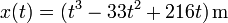
entre 
y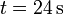 
.
- Calcule la velocidad y la aceleración de este movimiento.
- ¿Cuál es la máxima distancia de la posición inicial a la que llega a encontrarse la partícula? ¿Cuánto vale el desplazamiento neto a lo largo del intervalo? ¿Y la distancia total recorrida?
- ¿Cuánto valen la máxima y la mínima rapidez de este movimiento?
2 Velocidad y aceleración
2.1 Velocidad
La velocidad instantánea es igual a la derivada de la posición respecto al tiempo
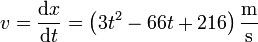
2.2 Aceleración
Derivando de nuevo hallamos la aceleración instantánea
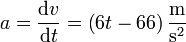
3 Distancia y desplazamiento
3.1 Máxima distancia
El punto de partida se encuentra en
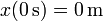
La máxima distancia de este punto se encuentra en el momento en el que la velocidad instantánea se anula (a partir de ahí vuelve a acercarse a la posición inicial. También puede ocurrir que la máxima distancia se encuentre al final del intervalo.
La velocidad instantánea se anula en
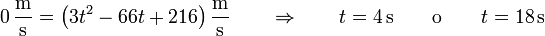
La posición en esos dos instantes se encuentra en
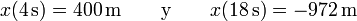
Al final del intervalo se cumple
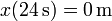
esto es, retorna a su posición inicial.
Por tanto la partícula parte del origen, avanza hacia valores positivos de x, hasta llegar a una distancia de 400 m. A partir de ahí retrocede, volviendo a pasar por la posición inicial (haciendo x(t) = 0 se ve que esto ocurre en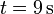 
) y llega a estar a 
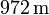a la izquierda. Ahí se detiene, vuelve a avanzar y finalmente acaba en la posición inicial.
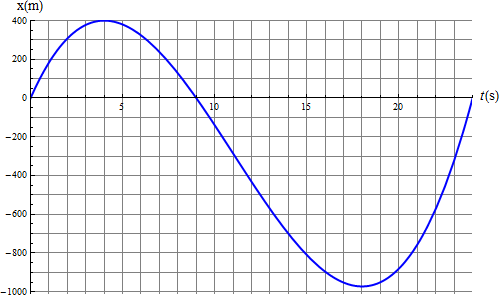
La máxima distancia de la posición inicial es entonces
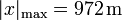
3.2 Desplazamiento
El desplazamiento es neto es la diferencia entre la posición final y la inicial
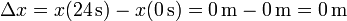
3.3 Distancia recorrida
La distancia total recorrida no coincide con el desplazamiento neto, ya que la partícula va y viene en su movimiento.
De los resultados del apartado anterior tenemos que la partícula avanza 400 m, luego retrocede esos mismos 400 m y hace 972 m. Por último vuelve a recorrer de nuevo los 972 m hasta la posición original. la distancia total recorrida es
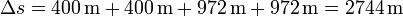
Si no hubiéramos hallado previamente estas cantidades podemos calcular la distancia total recorrida integrando la rapidez
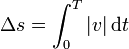
El valor absoluto de la velocidad se obtiene cambiando el signo de la velocidad en los tramos en que es negativa, lo que nos da
