Entrar Página Discusión Historial Go to the site toolbox

Ejemplo de movimiento expresado en polares

De Laplace

(Diferencias entre revisiones)
(→Identificación del movimiento)
(→Identificación del movimiento)
Línea 111: Línea 111:
vemos que
vemos que
-
<math>\vec{r}_c = \frac{A}{2}\vec{\imath}</math>
+
<center><math>\vec{r}_c = \frac{A}{2}\vec{\imath}</math></center>
que es evidentemente un punto fijo.
que es evidentemente un punto fijo.

Revisión de 10:07 12 oct 2011

Contenido

1 Enunciado

Una partícula describe una curva cuya ecuación en coordenadas polares es

\rho = A\cos(\omega t)\qquad\qquad \varphi = \omega t
  1. Calcule la velocidad y la aceleración en cada instante.
  2. Halle las componentes intrínsecas de la aceleración para todo t.
  3. Calcule el radio y el centro de curvatura en todo momento.
  4. ¿De qué tipo de movimiento se trata?

2 Velocidad y aceleración

2.1 Velocidad

La expresión de la velocidad empleando coordenadas polares es

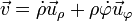
\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\varphi}\vec{u}_\varphi

donde, en este caso

\rho = A\cos(\omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\omega A\,\mathrm{sen}(\omega t)\qquad\qquad\varphi = \omega t\qquad \dot{\varphi}\equiv\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega

que, sustituyendo nos da

\vec{v}=\omega A\left(-\mathrm{sen}(\omega t)\vec{u}_\rho+\cos(\omega t)\vec{u}_\varphi\right)

2.2 Aceleración

La expresión correspondiente para la aceleración es

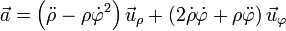
\vec{a}=\left(\ddot{\rho}-\rho\dot{\varphi}^2\right)\vec{u}_\rho + \left(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi}\right)\vec{u}_\varphi

siendo

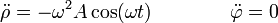
\ddot{\rho}=-\omega^2 A\cos(\omega t)\qquad\qquad \ddot{\varphi}=0

lo que nos da la aceleración

\vec{a}= -2\omega^2 A\cos(\omega t)\vec{u}_\rho-2\omega^2 A\,\mathrm{sen}(\omega t)\vec{u}_\varphi

3 Componentes intrínsecas

3.1 Tangencial

Una vez que tenemos la velocidad y la aceleración podemos hallar la aceleración tangencial algebraicamente

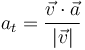
a_t = \frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}

o bien a partir de la rapidez

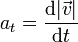
a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}

Para emplear el segundo método, calculamos en primer lugar la rapidez

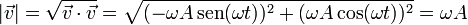
|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{(-\omega A\,\mathrm{sen}(\omega t))^2+(\omega A\cos(\omega t))^2}=\omega A

El movimiento es entonces uniforme y por tanto

a_t = \frac{\mathrm{d}\ }{\mathrm{d}t}(\omega A) = 0

Algebraicamente puede verse que la velocidad y la aceleración son ortogonales en todo momento, y por tanto se anula la componente tangencial.

3.2 Normal

Si la aceleración tangencial es nula, la aceleración normal es toda la que hay

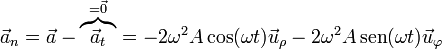
\vec{a}_n = \vec{a}-\overbrace{\vec{a}_t}^{=\vec{0}} = -2\omega^2 A\cos(\omega t)\vec{u}_\rho-2\omega^2 A\,\mathrm{sen}(\omega t)\vec{u}_\varphi

En módulo la aceleración normal vale

a_n = \sqrt{\vec{a}_n\cdot\vec{a}_n}= \sqrt{(2\omega^2 A\cos(\omega t))^2+(-2\omega^2 A\,\mathrm{sen}(\omega t))^2} = 2\omega^2A

4 Radio y centro de curvatura

4.1 Radio de curvatura

Conocidas la aceleración normal y la rapidez, hallamos el radio de curvatura.

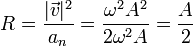
R = \frac{|\vec{v}|^2}{a_n} = \frac{\omega^2A^2}{2\omega^2 A}=\frac{A}{2}

Vemos que resulta un radio de curvatura constante.

4.2 Centro de curvatura

El centro de curvatura lo obtenemos a partir del vector de posición, el vector normal y el radio de curvatura

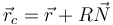
\vec{r}_c = \vec{r}+R\vec{N}

El vector normal en este caso es el unitario en la dirección y sentido de la aceleración normal

\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|} = -\cos(\omega t)\vec{u}_\rho-\,\mathrm{sen}(\omega t)\vec{u}_\varphi

mientras que el vector de posición vale

\vec{r} = \rho\vec{u}_\rho = A\cos(\omega t)\vec{u}_\rho

lo que nos da el centro de curvatura

\vec{r}_c = \frac{A}{2}\cos(\omega t)\vec{u}_\rho-\frac{A}{2}\,\mathrm{sen}(\omega t)\vec{u}_\varphi

5 Identificación del movimiento

Hemos obtenido que:

  • El movimiento es plano
  • El radio de curvatura es constante
  • La rapidez es constante

Estas tres propiedades identifican el movimiento como circular uniforme. La partícula describe circunferencias a ritmo constante alrededor de un punto fijo que es el centro de curvatura.

A la vista de la expresión del centro de curvatura

\vec{r}_c = \frac{A}{2}\cos(\omega t)\vec{u}_\rho-\frac{A}{2}\,\mathrm{sen}(\omega t)\vec{u}_\varphi

parecería que este punto es variable en el tiempo. Sin embargo, no es así. Si en lugar de la base vectorial de polares empleamos la de cartesianas, relacionada con la otra por

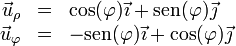
\begin{array}{rcl} \vec{u}_\rho & = & \cos(\varphi)\vec{\imath}+\mathrm{sen}(\varphi)\vec{\jmath} \\ \vec{u}_\varphi & = & -\mathrm{sen}(\varphi)\vec{\imath}+\cos(\varphi)\vec{\jmath} \end{array}

vemos que

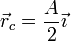
\vec{r}_c = \frac{A}{2}\vec{\imath}

que es evidentemente un punto fijo.

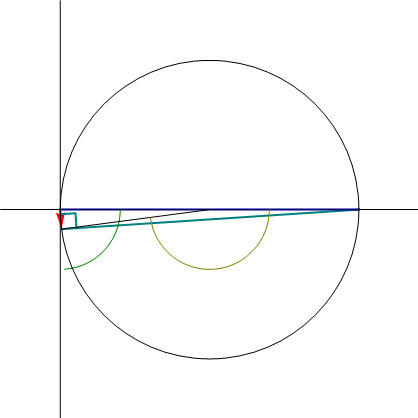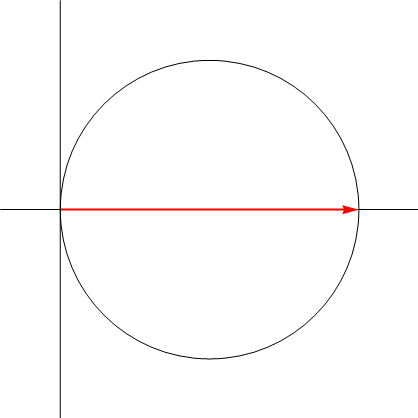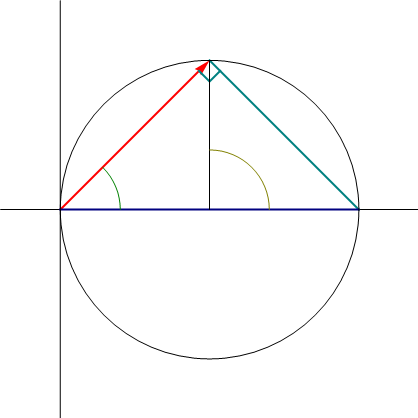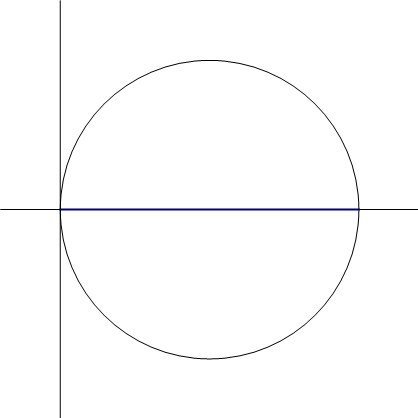
Podemos describir la trayectoria sin recurrir a su expresión en cartesianas, observando que en cada instante el vector de posición forma un ángulo 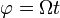\varphi=\Omega t con el eje OX y tiene por módulo A\cos(\varphi). Esto quiere decir que se puede considerar un cateto de un triángulo rectángulo de ángulo \varphi. La hipotenusa de este triángulo mide A para todo instante y se encuentra sobre el eje OX.

Archivo:circunferencia-excentrica-01.png

Ahora bien, según se ve en el estudio del arco capaz si tenemos un triángulo cuya hipotenusa AB es fija y cuyo ángulo en el vértice va variando, el tercer vértice P describe un arco de circunferencia de radio A / 2. El ángulo que forma CP con el eje OX es el doble del del vértice θ = 2Ωt.

Archivo:circunferencia-excentrica-02.png

Vemos entonces que la partícula efectivamente describe una circunferencia con velocidad angular constante, siendo su velocidad angular \vec{\omega}=2\Omega\vec{k}

Archivo:circunferencia-excentrica.gif
Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplo_de_movimiento_expresado_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace