Entrar Página Discusión Historial Go to the site toolbox

Ejemplo de movimiento expresado en polares

De Laplace

(Diferencias entre revisiones)
Línea 37: Línea 37:
==Componentes intrínsecas==
==Componentes intrínsecas==
===Tangencial===
===Tangencial===
 +
Una vez que tenemos la velocidad y la aceleración podemos hallar la aceleración tangencial algebraicamente
 +
 +
<center><math>a_t = \frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}</math></center>
 +
 +
o bien a partir de la rapidez
 +
 +
<center><math>a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}</math></center>
 +
 +
Para emplear el segundo método, calculamos en primer lugar la rapidez
 +
 +
<center><math>|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{(-\omega A\,\mathrm{sen}(\omega t))^2+(\omega A\cos(\omega t))^2}=\omega A</math></center>
 +
 +
El movimiento es entonces uniforme y por tanto
 +
 +
<center><math>a_t = \frac{\mathrm{d}\ }{\mathrm{d}t}(\omega A) = 0</math></center>
 +
 +
Algebraicamente puede verse que la velocidad y la aceleración son ortogonales en todo momento, y por tanto se anula la componente tangencial.
 +
===Normal===
===Normal===
 +
Si la aceleración tangencial es nula, la aceleración normal es toda la que hay
 +
 +
<center><math>\vec{a}_n = \vec{a}-\overbrace{\vec{a}_t}^{=\vec{0}} = -2\omega^2 A\cos(\omega t)\vec{u}_\rho-2\omega^2 A\,\mathrm{sen}(\omega t)\vec{u}_\varphi</math></center>
 +
 +
En módulo la aceleración normal vale
 +
 +
<center><math>a_n = \sqrt{\vec{a}_n\cdot\vec{a}_n}= \sqrt{(2\omega^2 A\cos(\omega t))^2+(-2\omega^2 A\,\mathrm{sen}(\omega t))^2} = 2\omega^2A</math></center>
 +
==Radio y centro de curvatura==
==Radio y centro de curvatura==
===Radio de curvatura===
===Radio de curvatura===

Revisión de 23:36 11 oct 2011

Contenido

1 Enunciado

Una partícula describe una curva cuya ecuación en coordenadas polares es

\rho = A\cos(\omega t)\qquad\qquad \varphi = \omega t
  1. Calcule la velocidad y la aceleración en cada instante.
  2. Halle las componentes intrínsecas de la aceleración para todo t.
  3. Calcule el radio y el centro de curvatura en todo momento.
  4. ¿De qué tipo de movimiento se trata?

2 Velocidad y aceleración

2.1 Velocidad

La expresión de la velocidad empleando coordenadas polares es

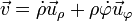
\vec{v}=\dot{\rho}\vec{u}_\rho + \rho\dot{\varphi}\vec{u}_\varphi

donde, en este caso

\rho = A\cos(\omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\omega A\,\mathrm{sen}(\omega t)\qquad\qquad\varphi = \omega t\qquad \dot{\varphi}\equiv\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega

que, sustituyendo nos da

\vec{v}=\omega A\left(-\mathrm{sen}(\omega t)\vec{u}_\rho+\cos(\omega t)\vec{u}_\varphi\right)

2.2 Aceleración

La expresión correspondiente para la aceleración es

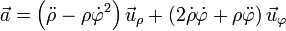
\vec{a}=\left(\ddot{\rho}-\rho\dot{\varphi}^2\right)\vec{u}_\rho + \left(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi}\right)\vec{u}_\varphi

siendo

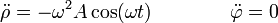
\ddot{\rho}=-\omega^2 A\cos(\omega t)\qquad\qquad \ddot{\varphi}=0

lo que nos da la aceleración

\vec{a}= -2\omega^2 A\cos(\omega t)\vec{u}_\rho-2\omega^2 A\,\mathrm{sen}(\omega t)\vec{u}_\varphi

3 Componentes intrínsecas

3.1 Tangencial

Una vez que tenemos la velocidad y la aceleración podemos hallar la aceleración tangencial algebraicamente

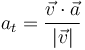
a_t = \frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}

o bien a partir de la rapidez

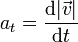
a_t = \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}

Para emplear el segundo método, calculamos en primer lugar la rapidez

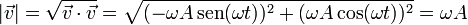
|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{(-\omega A\,\mathrm{sen}(\omega t))^2+(\omega A\cos(\omega t))^2}=\omega A

El movimiento es entonces uniforme y por tanto

a_t = \frac{\mathrm{d}\ }{\mathrm{d}t}(\omega A) = 0

Algebraicamente puede verse que la velocidad y la aceleración son ortogonales en todo momento, y por tanto se anula la componente tangencial.

3.2 Normal

Si la aceleración tangencial es nula, la aceleración normal es toda la que hay

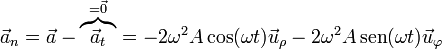
\vec{a}_n = \vec{a}-\overbrace{\vec{a}_t}^{=\vec{0}} = -2\omega^2 A\cos(\omega t)\vec{u}_\rho-2\omega^2 A\,\mathrm{sen}(\omega t)\vec{u}_\varphi

En módulo la aceleración normal vale

a_n = \sqrt{\vec{a}_n\cdot\vec{a}_n}= \sqrt{(2\omega^2 A\cos(\omega t))^2+(-2\omega^2 A\,\mathrm{sen}(\omega t))^2} = 2\omega^2A

4 Radio y centro de curvatura

4.1 Radio de curvatura

4.2 Centro de curvatura

5 Identificación del movimiento

Obtenido de "http://tesla.us.es/wiki/index.php/Ejemplo_de_movimiento_expresado_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace