Ejemplo de movimiento expresado en polares
De Laplace
(Diferencias entre revisiones)
(→Velocidad y aceleración) |
|||
| Línea 17: | Línea 17: | ||
donde, en este caso | donde, en este caso | ||
| - | <center><math>\rho = A\cos(\omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\omega A\,\mathrm{sen}(\omega t)</math> | + | <center><math>\rho = A\cos(\omega t)\qquad\dot{\rho}\equiv\frac{\mathrm{d}\rho}{\mathrm{d}t}=-\omega A\,\mathrm{sen}(\omega t)</math></center> |
| - | <math>varphi = \omega t\qquad \dot{\varphi}\equiv\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega</math></center> | + | <center><math>\varphi = \omega t\qquad \dot{\varphi}\equiv\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\omega</math></center> |
que, sustituyendo nos da | que, sustituyendo nos da | ||
| Línea 27: | Línea 27: | ||
===Aceleración=== | ===Aceleración=== | ||
| + | |||
==Componentes intrínsecas== | ==Componentes intrínsecas== | ||
===Tangencial=== | ===Tangencial=== | ||
Revisión de 21:01 11 oct 2011
Contenido |
1 Enunciado
Una partícula describe una curva cuya ecuación en coordenadas polares es

- Calcule la velocidad y la aceleración en cada instante.
- Halle las componentes intrínsecas de la aceleración para todo t.
- Calcule el radio y el centro de curvatura en todo momento.
- ¿De qué tipo de movimiento se trata?
2 Velocidad y aceleración
2.1 Velocidad
La expresión de la velocidad empleando coordenadas polares es
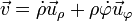
donde, en este caso


que, sustituyendo nos da






