Ejemplo de operaciones con dos vectores
De Laplace
(Diferencias entre revisiones)
| Línea 25: | Línea 25: | ||
==Área== | ==Área== | ||
| + | Podemos hallar el área a partir de lo que ya sabemos | ||
| + | |||
| + | <center><math>S = |\vec{v}||\vec{a}||\mathrm{sen}(\alpha)| = 30.0</math></center> | ||
| + | |||
| + | o bien a partir del producto vectorial | ||
| + | |||
| + | <center><math>\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 2.0 & 3.5 & -4.2 \\ 4.5 & -2.2 & 1.5\end{matrix}\right| = -3.99\vec{\imath}-21.9\vec{\jmath} -20.2\vec{k}</math></center> | ||
| + | |||
| + | cuyo módulo vale | ||
| + | |||
| + | <center><math>S = \sqrt{(-3.99)^2+(-21.9)^2+(20.15)^2} = 30.0</math></center> | ||
==Descomposición== | ==Descomposición== | ||
| + | Para descomponer el vector <math>\vec{a}</math> aplicamos | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 16:37 8 oct 2011
Contenido |
1 Enunciado
Dados los vectores

- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
 como suma de dos vectores, uno paralelo a
como suma de dos vectores, uno paralelo a  y otro ortogonal a él.
y otro ortogonal a él.
2 Ángulo
Obtenemos el ángulo a partir del producto escalar de los dos vectores
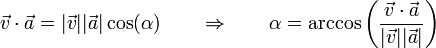
Tenemos que
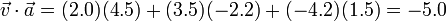
y que
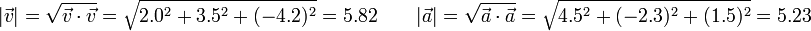
lo que nos da
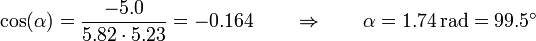
3 Área
Podemos hallar el área a partir de lo que ya sabemos
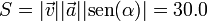
o bien a partir del producto vectorial
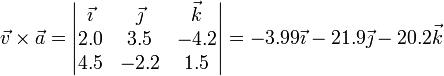
cuyo módulo vale
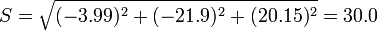
4 Descomposición
Para descomponer el vector  aplicamos
aplicamos





