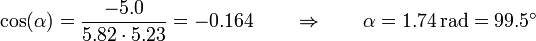Ejemplo de operaciones con dos vectores
De Laplace
(Diferencias entre revisiones)
| Línea 15: | Línea 15: | ||
<center><math>\vec{v}\cdot\vec{a}=(2.0)(4.5)+(3.5)(-2.2)+(-4.2)(1.5)=-5.0</math></center> | <center><math>\vec{v}\cdot\vec{a}=(2.0)(4.5)+(3.5)(-2.2)+(-4.2)(1.5)=-5.0</math></center> | ||
| + | |||
| + | y que | ||
| + | |||
| + | <center><math>|\vec{v}| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{2.0^2+3.5^2+(-4.2)^2} = 5.82\qquad |\vec{a}| = \sqrt{\vec{a}\cdot\vec{a}}=\sqrt{4.5^2+(-2.3)^2+(1.5)^2} = 5.23</math></center> | ||
| + | |||
| + | lo que nos da | ||
| + | |||
| + | <center><math>\cos(\alpha)=\frac{-5.0}{5.82\cdot 5.23}=-0.164\qquad\Rightarrow\qquad \alpha = 1.74\,\mathrm{rad}=99.5^\circ</math></center> | ||
| + | |||
==Área== | ==Área== | ||
| + | |||
==Descomposición== | ==Descomposición== | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 13:58 8 oct 2011
Contenido |
1 Enunciado
Dados los vectores
- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
como suma de dos vectores, uno paralelo a 
y otro ortogonal a él.
2 Ángulo
Obtenemos el ángulo a partir del producto escalar de los dos vectores
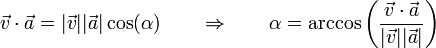
Tenemos que
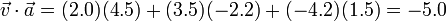
y que
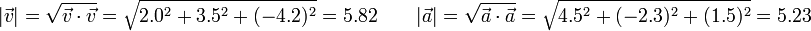
lo que nos da
