Derivada de un vector (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Enunciado == Un punto recorre una circunferencia de radio <math>R</math>, de modo que en cada instante el vector que une el centro de la circunferencia con el punto forma un …') |
(→Derivada respecto al tiempo) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 9: | Línea 9: | ||
=== Vector en función del ángulo <math>\alpha </math>=== | === Vector en función del ángulo <math>\alpha </math>=== | ||
| + | [[Imagen:F1_GIC_derivada_de_un_vector.png|right]] | ||
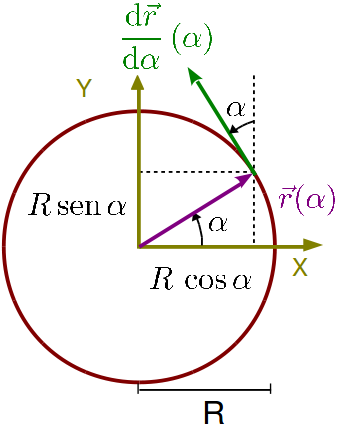
Proyectamos el vector de posición sobre los ejes <math>OX </math> y <math>OY </math> | Proyectamos el vector de posición sobre los ejes <math>OX </math> y <math>OY </math> | ||
<center> | <center> | ||
| Línea 42: | Línea 43: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | En la figura se muestra la dirección de este vector. Como el módulo de <math>\vec{r}(\alpha)</math> es constante (e igual a <math>R</math>), el vector derivada apunta en la dirección y sentido en que se mueve el extremo del vector <math>\vec{r}(\alpha)</math>. | ||
===Derivada respecto al tiempo === | ===Derivada respecto al tiempo === | ||
| Línea 72: | Línea 74: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | [[Categoría:Física I (G.I.A.)]] | ||
| + | [[Categoría:Física I (G.I.C.)]] | ||
última version al 17:03 7 oct 2011
Contenido |
1 Enunciado
Un punto recorre una circunferencia de radio R, de modo que en cada instante el vector que une el centro de la circunferencia con el punto forma un ángulo α con el eje OX.
- Encuentra la expresión del vector de posición del punto en función del ángulo α.
- Encuentra la expresión del vector de posición del punto en función del ángulo α.
- Si el ángulo α depende del tiempo como α = ωt, calcula la derivada del vector de posición respecto del tiempo.
2 Solución
2.1 Vector en función del ángulo α
Proyectamos el vector de posición sobre los ejes OX y OY
También podemos escribir el vector en términos de sus componentes cartesianas
2.2 Derivada del vector respecto de α
Los vectores de la base cartesiana no cambian cuando el ángulo α varía. Así pues, la derivada del vector 
es el vector
En la figura se muestra la dirección de este vector. Como el módulo de es constante (e igual a R), el vector derivada apunta en la dirección y sentido en que se mueve el extremo del vector .
2.3 Derivada respecto al tiempo
Ahora el ángulo α es una función del tiempo
α(t) = ωt
Aplicamos la regla de la cadena
Tenemos
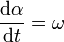
Por tanto
