Entrar Página Discusión Historial Go to the site toolbox

Cálculo numérico de la derivada del seno

De Laplace

(Diferencias entre revisiones)
(→Aproximación numérica)
(→Interpretación del resultado)
 
(3 ediciones intermedias no se muestran.)
Línea 119: Línea 119:
|}
|}
 +
Vemos entonces lo que está pasando. El límite, esto es, la derivada, no vale 1, sino &pi;/180 en <math>x=0^\circ</math>.
 +
 +
¿Por qué ocurre esto? Porque estamos midiendo el ángulo en grados. Las fórmulas
 +
 +
<center><math>\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{sen}(x)) = \cos(x)\qquad \frac{\mathrm{d}\ }{\mathrm{d}x}(\cos(x)) =\,\mathrm{sen}(x)</math></center>
 +
 +
solo valen si el ángulo se mide en ''radianes''.
 +
 +
Veamos como sería la demostración del resultado que hemos obtenido. Tenemos que
 +
 +
<center><math>180^\circ = \pi\,\mathrm{rad}\qquad\Rightarrow\qquad 1^\circ = \frac{\pi}{180}\,\mathrm{rad}</math></center>
 +
 +
y por tanto
 +
 +
<center><math>x^\circ = \frac{\pi}{180}x\,\mathrm{rad}</math></center>
 +
 +
Lo que hemos calculado es entonces
 +
 +
<center><math>\left.\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\mathrm{sen}\left(\frac{\pi}{180}x\right)\right)\right|_{x=0} = \frac{\pi}{180}\left.\cos\left(\frac{\pi}{180}x\right)\right|_{x=0}=\frac{\pi}{180}</math></center>
 +
 +
en total coincidencia con el resultado numérico.
[[Categoría:Problemas de herramientas matemáticas (GIE)]]
[[Categoría:Problemas de herramientas matemáticas (GIE)]]

última version al 22:13 5 oct 2011

Contenido

1 Enunciado

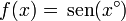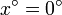Se trata de calcular la derivada de f(x)=\,\mathrm{sen}(x^\circ) para x^\circ=0^\circ.

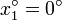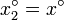  1. Exprese el cociente Δf / Δx, cuando x_1^\circ=0^\circ y x_2^\circ=x^\circ.
  2. Calcule numéricamente el cociente anterior para 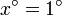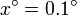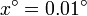x^\circ=1^\circ, x^\circ=0.1^\circ, x^\circ=0.01^\circ,… hasta 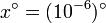x^\circ=(10^{-6})^\circ. ¿A cuanto tiende el límite?
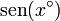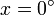  3. Multiplique los resultados anteriores por 180. A la vista de los resultados, ¿cuanto vale la derivada de \mathrm{sen}(x^\circ) en x=0^\circ?

2 Cociente incremental

La derivada de una función equivale al límite del cociente entre incrementos cuando estos tienden a cero

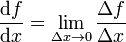
\frac{\mathrm{d}f}{\mathrm{d}x} = \lim_{\Delta x\to 0} \frac{\Delta f}{\Delta x}

En nuestro caso, consideramos un incremento entre 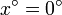x^\circ = 0^\circ y un cierto valor del ángulo

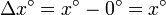
\Delta x^\circ = x^\circ - 0^\circ = x^\circ

mientras que el incremento en la función es

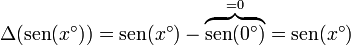
\Delta(\mathrm{sen}(x^\circ))=\mathrm{sen}(x^\circ)-\overbrace{\mathrm{sen}(0^\circ)}^{=0}= \mathrm{sen}(x^\circ)

Por tanto, el cociente entre incrementos se reduce a

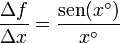
\frac{\Delta f}{\Delta x}=\frac{\mathrm{sen}(x^\circ)}{x^\circ}

3 Aproximación numérica

Calculamos entonces los valores del cociente incremental para valores cada vez más pequeños del argumento

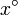
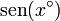
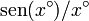
x^\circ \mathrm{sen}(x^\circ) \mathrm{sen}(x^\circ)/x^\circ
1 0.017452406437283512819 0.017452406437283512819
0.1 0.001745328365898308836 0.017453283658983088358
0.01 0.001745329243133368033 0.017453292431333680334
0.001 0.000174532925190571996 0.017453292519057199614
0.0001 0.000017453292519934435 0.017453292519934434808
0.00001 0.000001745329251994321 0.017453292519943207160
0.000001 0.000000174532925199433 0.017453292519943294883

Vemos que efectivamente el cociente converge, pero desde luego no a 1, que es lo que cabría esperar (si la derivada del seno es el coseno, al hacer x = 0, nos debería salir 1).

4 Interpretación del resultado

Para interpretar el resultado, seguimos la sugerencia del enunciado y multiplicamos el resultado por 180, a ver qué sale

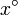
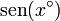
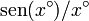
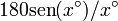
x^\circ \mathrm{sen}(x^\circ) \mathrm{sen}(x^\circ)/x^\circ 180 \mathrm{sen}(x^\circ)/x^\circ
1 0.017452406437283512819 0.017452406437283512819 3.1414331587110323075
0.1 0.001745328365898308836 0.017453283658983088358 3.1415910586169559044
0.01 0.001745329243133368033 0.017453292431333680334 3.1415926376400624601
0.001 0.000174532925190571996 0.017453292519057199614 3.1415926534302959304
0.0001 0.000017453292519934435 0.017453292519934434808 3.1415926535881982654
0.00001 0.000001745329251994321 0.017453292519943207160 3.1415926535897772887
0.000001 0.000000174532925199433 0.017453292519943294883 3.1415926535897930790
··· ··· ··· ···
0 0 π/180 π

Vemos entonces lo que está pasando. El límite, esto es, la derivada, no vale 1, sino π/180 en 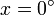x=0^\circ.

¿Por qué ocurre esto? Porque estamos midiendo el ángulo en grados. Las fórmulas

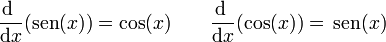
\frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{sen}(x)) = \cos(x)\qquad \frac{\mathrm{d}\ }{\mathrm{d}x}(\cos(x)) =\,\mathrm{sen}(x)

solo valen si el ángulo se mide en radianes.

Veamos como sería la demostración del resultado que hemos obtenido. Tenemos que

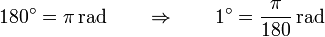
180^\circ = \pi\,\mathrm{rad}\qquad\Rightarrow\qquad 1^\circ = \frac{\pi}{180}\,\mathrm{rad}

y por tanto

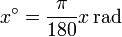
x^\circ = \frac{\pi}{180}x\,\mathrm{rad}

Lo que hemos calculado es entonces

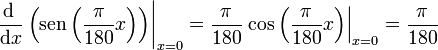
\left.\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\mathrm{sen}\left(\frac{\pi}{180}x\right)\right)\right|_{x=0} = \frac{\pi}{180}\left.\cos\left(\frac{\pi}{180}x\right)\right|_{x=0}=\frac{\pi}{180}

en total coincidencia con el resultado numérico.

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_num%C3%A9rico_de_la_derivada_del_seno"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 22:13, 5 oct 2011. - Esta página ha sido visitada 3.032 veces. - Aviso legal - Acerca de Laplace