Vértices de un tetraedro (G.I.A.)

De Laplace

(Diferencias entre revisiones)

última version al 16:07 4 oct 2011

1 Enunciado

Los puntos $O$ , $A$ , $B$ y $C$ son los vértices del tetraedro regular cuyas caras son triángulos equiláteros con lados de longitud $λ$ . A partir de las aristas de dicho tetraedro se definen los siguientes vectores libres:

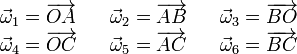
$\begin{array}{lllll} \vec{\omega}_1=\overrightarrow{OA} && \vec{\omega}_2=\overrightarrow{AB} && \vec{\omega}_3=\overrightarrow{BO}\\ \vec{\omega}_4=\overrightarrow{OC} && \vec{\omega}_5=\overrightarrow{AC} && \vec{\omega}_6=\overrightarrow{BC} \end{array}$

Para describirlos analíticamente se adopta un sistema de referencia cartesiano $O X Y Z$ , tal que la cara $O A B$ del tetraedro está contenida en el plano $O X Y$ , y el vértice $B$ es un punto del eje $O Y$ (ver figura). Utilizando las herramientas del Álgebra Vectorial, determina las coordenadas cartesianas de los vértices del tetraedro.

2 Solución

De la figura podemos obtener las coordenadas de los puntos $O$ y $B$ ,

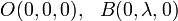
$O(0,0,0),\,\,\,\,B(0,\lambda,0)$

Para averiguar las coordenadas del punto $A$ nos fijamos en el dibujo. Las caras del tetraedro son triángulos equiláteros, por los cual sus ángulos son todos $π / 3$ . Expresado en la base cartesiana asociada al triedro, el vector 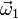$\vec{\omega}_1$ es

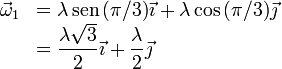
$\begin{array}{ll} \vec{\omega}_1 &= \lambda\,\mathrm{sen}\,{(\pi/3)}\vec{\imath} + \lambda\cos{(\pi/3)}\vec{\jmath} \\ &= \dfrac{\lambda\sqrt{3}}{2}\vec{\imath} + \dfrac{\lambda}{2}\vec{\jmath} \end{array}$

y las coordenadas del punto $A$ son

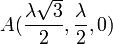
$A(\dfrac{\lambda\sqrt{3}}{2},\dfrac{\lambda}{2},0)$

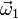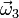Las componentes de los vectores $\vec{\omega}_1$ y $\vec{\omega}_3$ son

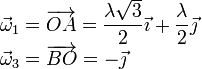
$\begin{array}{l} \vec{\omega}_1 = \overrightarrow{OA} = \dfrac{\lambda\sqrt{3}}{2}\vec{\imath} + \dfrac{\lambda}{2}\vec{\jmath}\\ \vec{\omega}_3 = \overrightarrow{BO} = -\vec{\jmath}\\ \end{array}$

Las coordenadas del punto $C (x, y, z)$ pueden obtenerse calculando el vector 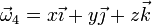$\vec{\omega}_4=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$ . De este vector conocemos su módulo

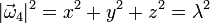
$|\vec{\omega}_4|^2 = x^2+y^2+z^2 = \lambda^2$

Como las caras son triángulos equiláteros, todos los ángulos entre las aristas son de $π / 3$ , por lo cual también conocemos los productos escalares con los vectores 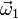$\vec{\omega}_1$ y $\vec{\omega}_3$

$\begin{array}{l} \vec{\omega}_4\cdot\vec{\omega}_1 = \lambda^2\cos(\pi/3) = \lambda^2/2\\ \vec{\omega}_4\cdot(-\vec{\omega}_3) = -\lambda^2\cos(\pi/3) = -\lambda^2/2 \end{array}$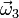

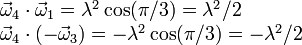
Por otro lado podemos expresar estos productos escalares en función de las componentes de los vectores

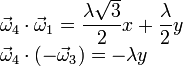
$\begin{array}{l} \vec{\omega}_4\cdot\vec{\omega}_1 = \dfrac{\lambda\sqrt{3}}{2}x + \dfrac{\lambda}{2}y\\ \vec{\omega}_4\cdot(-\vec{\omega}_3) = -\lambda y \end{array}$

Estas expresiones nos proporcionan tres ecuaciones con tres incógnitas

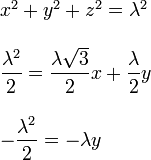
$\begin{array}{l} x^2 + y^2 + z^2 = \lambda^2\\ \\ \dfrac{\lambda^2}{2} = \dfrac{\lambda\sqrt{3}}{2}x +\dfrac{\lambda}{2}y\\ \\ -\dfrac{\lambda^2}{2} = -\lambda y \end{array}$

Resolviéndolo obtenemos las coordenadas de $C$

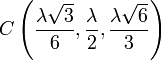
$C\left(\dfrac{\lambda\sqrt{3}}{6},\dfrac{\lambda}{2},\dfrac{\lambda\sqrt{6}}{3}\right)$

Hay que señalar que hemos descartado la otra solución de la primera ecuación 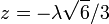$z=-\lambda\sqrt{6}/3$ . Este caso representa un tetraedro simétrico al del dibujo respecto al plano $O X Y$ , es decir, con el vértice $C$ por debajo del plano.

@@ Línea 90: / Línea 90: @@
 representa un tetraedro simétrico al del dibujo
 respecto al plano <math>OXY</math>, es decir, con el vértice <math>C</math> por debajo del plano.
+[[Categoría:Vectores libres|0]]
+[[Categoría:Física I (G.I.A.)]]
+[[Categoría:Física I (G.I.T.I.)]]
+[[Categoría:Física I (G.I.C.)]]

Vértices de un tetraedro (G.I.A.)

De Laplace

última version al 16:07 4 oct 2011

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES