Ejemplo de estimación de longitudes y volúmenes
De Laplace
(→Caso del oro) |
|||
| (Una edición intermedia no se muestra.) | |||
| Línea 70: | Línea 70: | ||
<center><math>0.015\,\mathrm{m}^2 < S < 0.016\,\mathrm{m}^2</math></center> | <center><math>0.015\,\mathrm{m}^2 < S < 0.016\,\mathrm{m}^2</math></center> | ||
| - | Vemnos que resulta un cubo con casi la mitad de arista que en el caso del aluminio. | + | Vemnos que resulta un cubo con casi la mitad de arista que en el caso del aluminio. De hecho podemos obtener la proporcioón entre longitud y entre áreas de manera general, sin saber la cantidad exacta de metal |
| + | |||
| + | <center><math>\frac{L_\mathrm{Al}}{L_\mathrm{Au}}=\left(\frac{\rho_\mathrm{Au}}{\rho_\mathrm{Al}}\right)^{1/3} = 1.92</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\frac{S_\mathrm{Al}}{S_\mathrm{Au}}=\left(\frac{\rho_\mathrm{Au}}{\rho_\mathrm{Al}}\right)^{2/3} = 3.71</math></center> | ||
| + | |||
[[Categoría:Problemas de introducción a la física (GIE)]] | [[Categoría:Problemas de introducción a la física (GIE)]] | ||
última version al 11:42 24 sep 2011
Contenido |
1 Enunciado
Se tiene un bloque de aluminio de forma cúbica cuya masa es aproximadamente 2.5 kg. Estime el valor de la arista del cubo, así como su superficie lateral. Si se sabe que la incertidumbre de la medida de la masa es de 100 g, ¿entre qué valores se hallarán la arista y el área lateral?
¿Y si en vez de aluminio fuera oro?
2 Arista
El volumen de un cubo es la arista al cubo, por tanto
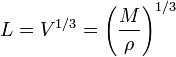
Necesitamos la densidad de masa del aluminio. Sabemos que es un metal ligero cuya densidad es más o menos la de las rocas (unos 3 g/cm³) pero lo consultamos en la red y vemos que vale
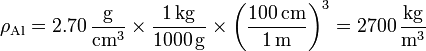
Sustituyendo los valores de la masa y la densidad quedaría
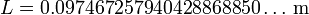
Sin embargo, no es lógico un resultado con tantos decimales, cuando de los datos del problema, la densidad se da con 3 cifras significativas y la masa solo con 2. Si no sabemos la tercera cifra significativa de la masa, ¿cómo podemos esperar conocer la 12ª de la arista? Siendo coherentes, debemos mantener el número de cifras significativas en el menor de los de los datos (2, en este caso), por lo que
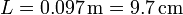
3 Área lateral
El área lateral es la de seis cuadrados de lado L o, directamente en función del volumen
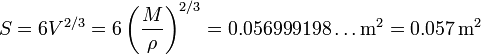
donde de nuevo hemos redondeado a 2 cifras significativas. En cm²
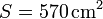
Obsérvese que el número de cifras significativas sigue siendo 2, aunque ahora la cantidad tiene tres dígitos.
4 Incertidumbres
Una mejor estimación de la expresión correcta lo obtenemos si conocemos la incertidumbre de la medida original, la cual se expresa mediante las bandas de error, de forma que
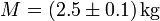
esto es, que el valor de la masa verifica, con gran probabilidad,
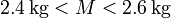
Tomando los valores extremos de este intervalo obtenemos el intervalo para la longitud
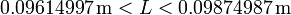
con lo que vemos que efectivamente tenemos una incertidumbre en la segunda cifra significativa (el tercer decimal). Por ello se expresará mejor como

Operando igualmente para el área lateral
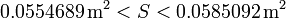
lo que se expresa, redondeando hasta la primera cifra incierta
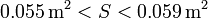
5 Caso del oro
Para un cubo de oro, el cálculo es análogo, salvo que el oro es mucho más denso que el aluminio (casi 20 toneladas por metro cúbico)
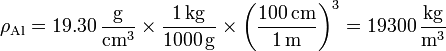
lo que nos da el intervalo de longitudes
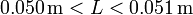
y de áreas laterales

Vemnos que resulta un cubo con casi la mitad de arista que en el caso del aluminio. De hecho podemos obtener la proporcioón entre longitud y entre áreas de manera general, sin saber la cantidad exacta de metal
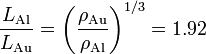
y






