Ejemplos de cálculo de dimensiones
De Laplace
(Página creada con '==Velocidad== La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto …') |
(→Velocidad) |
||
| Línea 1: | Línea 1: | ||
| + | ==Enunciado== | ||
| + | A partir de las relaciones definitorias | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Velocidad | ||
| + | ! Cantidad de movimiento | ||
| + | ! Aceleración | ||
| + | ! Fuerza | ||
| + | |- | ||
| + | | <math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}</math> | ||
| + | | <math>\vec{p}=m\vec{v}</math> | ||
| + | | <math>\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}</math> | ||
| + | | <math>\vec{F}=\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}</math> | ||
| + | |- | ||
| + | ! Trabajo | ||
| + | ! Potencia | ||
| + | ! Momento cinético | ||
| + | ! Momento de una fuerza | ||
| + | |- | ||
| + | | <math>W=\int_A^B\vec{F}\cdot\mathrm{d}\vec{r}</math> | ||
| + | | <math>P=\frac{\mathrm{d}W}{\mathrm{d}t}</math> | ||
| + | | <math>\vec{L}=\vec{r}\times\vec{p}</math> | ||
| + | | <math>\vec{M}=\vec{r}\times\vec{F}</math> | ||
| + | |} | ||
| + | |||
| + | determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades fundamentales de este sistema. | ||
| + | |||
==Velocidad== | ==Velocidad== | ||
La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es, | La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es, | ||
última version al 10:06 24 sep 2011
Contenido |
1 Enunciado
A partir de las relaciones definitorias
| Velocidad | Cantidad de movimiento | Aceleración | Fuerza |
|---|---|---|---|
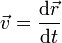
| 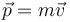
| 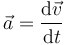
| 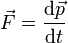
|
| Trabajo | Potencia | Momento cinético | Momento de una fuerza |
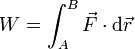
| 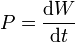
| 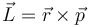
| 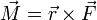
|
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el Sistema Internacional (SI) en función de las unidades fundamentales de este sistema.
2 Velocidad
La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es,
![[v] = \frac{[r]}{[t]} = L T^{-1}](/wiki/images/math/4/a/8/4a863b7095d58bec7e7ed807d4621882.png)
La unidad en el SI de velocidad es 1 m/s.
3 Cantidad de movimiento
La cantidad de movimiento es el producto de la masa por la velocidad, por lo que sus dimensiones serán las del producto de estas dos cantidades:
![[p]= [m][v]= MLT^{-1}\,](/wiki/images/math/c/c/f/ccf3c8fda602830730e68a41994ae67f.png)
La unidad SI de la cantidad de movimiento es 1 kg·m/s.
4 Aceleración
La aceleración es la derivada de la velocidad respecto al tiempo, por tanto
![[a] = \frac{[v]}{[t]} = \frac{LT^{-1}}{T}=LT^{-2}](/wiki/images/math/e/7/6/e7679e3620d075e018bcdb8854af18c6.png)
La unidad de aceleración en el SI será 1 m/s².
5 Fuerza
La fuerza se define como la derivada de la cantidad de movimiento (aunque también suele expresarse como el producto de la masa por la aceleración). Por ello
![[F] = \frac{[p]}{[t]} = \frac{MLT^{-1}}{T}=MLT^{-2}](/wiki/images/math/8/6/9/869bb07dc26bc625d804a015bb338ed7.png)
La unidad SI de la fuerza es el newton, que equivale a
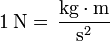
6 Trabajo
El trabajo se define a partir de una integral, esto es, una suma de muchas cantidades muy pequeñas. Las dimensiones de la integral son entonces las mismas que las de cada uno de los sumandos. Cada sumando es un trabajo diferencial, igual al producto escalar de una fuerza por un desplazamiento. Por ello
![[W]= [F][r] = (MLT^{-2})(L) = ML^2T^{-2}\,](/wiki/images/math/9/f/d/9fd0facc16f41aefea2ed7ee6941e93d.png)
Vemos que el trabajo posee dimensiones de masa por velocidad al cuadrado, que son las mismas de la energía cinética
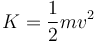

![[K] = [m][v]^2 = M(LT^{-1})^2 = ML^2T^{-2}\,](/wiki/images/math/2/8/2/2825419f6d391d2052235399add61cbb.png)
La unidad de trabajo en el sistema internacional es el julio, equivalente a

7 Potencia
La potencia es el cociente entre un trabajo diferencial y el tiempo diferencial en que se realiza. Las dimensiones las da también el cociente
![[P]=\frac{[W]}{[t]}=\frac{ML^2T^{-2}}{T}=ML^2T^{-3}](/wiki/images/math/b/0/5/b05e0f77f71f82a492d05e15992fe40c.png)
La unidad SI de potencia es el vatio, que equivale a

8 Momento cinético
El momento cinético es el producto vectorial de la posición por la cantidad de movimiento. Todo producto (de escalares, escalar, vectorial,…) tiene dimensiones del producto de las magnitudes, esto es,
![[L]=[r][p] = L(MLT^{-1}) = ML^2T^{-1}\,](/wiki/images/math/a/b/e/abe6f7e7a023fea1564aca52d322f5a0.png)
La unidad de momento cinético en el SI será 1 kg·m²/s.
9 Momento de una fuerza
Por último, el momento de una fuerza equivale al producto vectorial de un vector de posición (con dimensiones de distancia) y una fuerza
![[M] = [r][F] = (L)(MLT^{-2}) = ML^2T^{-2}\,](/wiki/images/math/5/d/4/5d4bf3a003e2a33f6c41bee7093e016b.png)
La unidad de momento en el SI es el newton por metro

Aunque esta unidad es equivalente a un julio, no se utiliza 1 J como unidad de momento de una fuerza, debido a que esta magnitud no representa trabajo, calor o energía, cantidades para las que se reserva el uso del julio.





