Cuatro planos conductores paralelos
De Laplace
(→Empleando los coeficientes de capacidad) |
(→Empleando los coeficientes de capacidad) |
||
| Línea 25: | Línea 25: | ||
Entre cada dos nodos consecutivos habrá un condensador, que al despreciar los efectos de borde (pues <math>L\gg a</math>) tienen por valores los de condensadores planos: | Entre cada dos nodos consecutivos habrá un condensador, que al despreciar los efectos de borde (pues <math>L\gg a</math>) tienen por valores los de condensadores planos: | ||
| + | |||
| + | <center>[[Imagen:circuito4placas1.gif]]</center> | ||
<center><math>\overline{C}_{12} = \frac{\varepsilon_0 L^2}{a}\equiv C</math>{{qquad}}{{qquad}}<math>\overline{C}_{23} = \frac{\varepsilon_0 L^2}{3a}=\frac{C}{3}</math>{{qquad}}{{qquad}}<math>\overline{C}_{3a} = \frac{\varepsilon_0 L^2}{2a}=\frac{C}{2}</math></center> | <center><math>\overline{C}_{12} = \frac{\varepsilon_0 L^2}{a}\equiv C</math>{{qquad}}{{qquad}}<math>\overline{C}_{23} = \frac{\varepsilon_0 L^2}{3a}=\frac{C}{3}</math>{{qquad}}{{qquad}}<math>\overline{C}_{3a} = \frac{\varepsilon_0 L^2}{2a}=\frac{C}{2}</math></center> | ||
Revisión de 09:29 3 jul 2008
Contenido |
1 Enunciado
).
Las placas exteriores se encuentran a tierra en todo instante.
- Inicialmente la segunda placa almacena una carga Q, mientras que la tercera está aislada y descargada. determine el potencial al que se encuentra cada placa, así como la carga que almacena cada una.
- Para el caso anterior, determine el campo eléctrico en todos los puntos entre las placas.
- Si ahora se conectan las dos placas intermedias, ¿cómo cambian las cargas y los potenciales de las distintas placas? ¿Y los campos eléctricos entre las placas?
- Determine la variación de energía entre el estado anterior y el posterior a la conexión.
2 Solución
2.1 Cargas y potenciales iniciales
Existen dos formas alternativas de enfocar este problema: relacionar directamente las cargas con los potenciales a través de los coeficientes de capacidad, o bien analizar y resolver el circuito equivalente.
En ambos casos, interesa describir el circuito equivalente al sistema,
que nos da las capacidades y autocapacidades,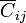 
, las cuales nos permiten calcular los coeficientes de capacidad, 
.
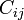2.1.1 Empleando los coeficientes de capacidad
El circuito equivalente al sistema está formado, de entrada, por cuatro nodos correspondientes a cada conductor.
Entre cada dos nodos consecutivos habrá un condensador, que al despreciar los efectos de borde (pues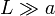 
) tienen por valores los de condensadores planos:
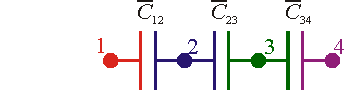
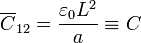
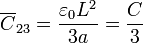
No lo habrá entre placas que estén separados por otra placa, ya que estarán apantallados. Así, no habrá condensador que una el conductor 1 con el 3 o el 4, ni el 2 con el 4.
Aparte habría que añadir un condensador entre cada nodo y tierra. De nuevo, estarán ausentes los de aquellos nodos de los cuales no pueda haber líneas que vayan al infinito.
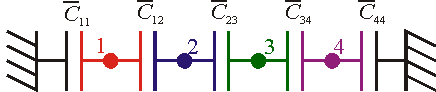
Estos son el 2 y el 3, que se encuentran apantallados por el 1 y el 4. Si estarían los correspondientes a estos dos,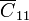 
y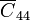 
. No conocemos los valores de estas cantidades, pero, como veremos, esto no constituye un problema.
Una vez situados los condensadores, tenemos que añadir una conexión a una fuente por cada conductor que esté a potencial fijado. Éstos son el 1 y el 4, que están a tierra.
Ahora bien, al fijar en cero el potencial de estos dos nodos y ser nulo el potencial del infinito, estamos efectivamente cortocircuitando los condensadores 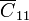y 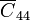. Estos condensadores estarán descargados en todo instante y no afectarán a ningún resultado. Podemos, por tanto, limitarnos a considerar los tres condensadores planos cuyas capacidades son conocidas.
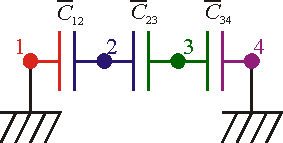
Además de los generadores de tensión, tenemos los generadores de carga conectados a cada nodo cuya carga este fijada. Estos son el nodo 2, que almacena una carga Q y el 3, que está descargado. Por ser el conductor 3 uno aislado y descargado, podemos omitir el generador de carga correspondiente.
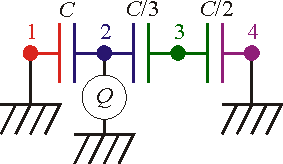
Por tanto, el sistema se compone de tres condensadores, dos conexiones a tierra y un generador de carga.
Las relaciones entre las cargas y los potenciales las obtenemos sumando las cargas de los distintos condensadores unidos a cada nodo. Esto nos da las relaciones
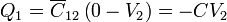
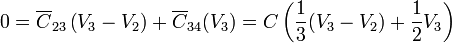
donde ya hemos sustituido directamente los cuatro datos
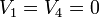
y hemos simplificado las expresiones usando la abreviatura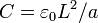 
.
Del sistema anterior, la segunda y la tercera ecuación proporcionan un sistema de dos ecuaciones con dos incógnitas, V2 y V3, que podemos escribir como
De la segunda obtenemos que
y sustituyendo en la primera
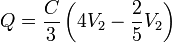
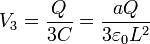
Conocidos estos dos potenciales hallamos las cargas de los conductores exteriores
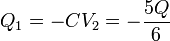
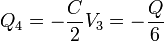
La carga total del sistema es nula
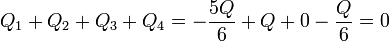
como corresponde a que en el exterior del sistema no haya campo eléctrico.
2.1.2 Empleando solo el circuito equivalente
Podemos determinar estas cargas y potenciales empleando exclusivamente el circuito equivalente.
Si nos centramos en el nodo 2, que almacena una carga Q, vemos que está conectado a tierra por dos ramas en paralelo. Una contiene un solo condensador, de capacidad C, y la otra dos condensadores en serie, de capacidades C / 2 y C / 3. El potencial de este nodo será
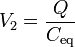
siendo la capacidad equivalente
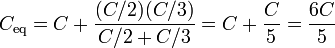
por lo que
Una vez que tenemos el potencial del nodo 2, podemos hallar la carga Q1, que se encuentra en la placa negativa de un condensador de capacidad C, sometido a una tensión V2. Por tanto
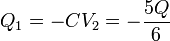
Análogamente obtenemos la carga Q4, que se encuentra en la placa negativa del condensador de la segunda rama, de capacidad equivalente C / 5, por lo que
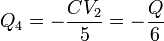
Conocido Q4 podemos hallar V3, ya que entre este nodo y tierra existe un condensador de capacidad C / 2, del cual conocemos la carga (que es − Q4). Por tanto
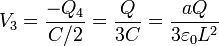
El resultado, lógicamente, coincide con el obtenido anteriormente.
