Curvas y peraltes (GIE)
De Laplace
(Diferencias entre revisiones)
(→Sin rozamiento) |
|||
| Línea 8: | Línea 8: | ||
En la curva, el coche realiza un movimiento circular uniforme. La aceleración de este movimiento es puramente normal. De acuerdo con la segunda ley de Newton nos queda | En la curva, el coche realiza un movimiento circular uniforme. La aceleración de este movimiento es puramente normal. De acuerdo con la segunda ley de Newton nos queda | ||
| - | <center><math>m\vec{g}+\vec{\ | + | <center><math>m\vec{g}+\vec{\Phi}=-m\frac{|\vec{v}|^2}{R}\vec{u}_\rho</math></center> |
siendo <math>\vec{u}_\rho</math> el vector unitario radial hacia afuera. El signo menos viene de que la aceleración normal es siempre hacia adentro de la curva. | siendo <math>\vec{u}_\rho</math> el vector unitario radial hacia afuera. El signo menos viene de que la aceleración normal es siempre hacia adentro de la curva. | ||
| Línea 14: | Línea 14: | ||
El peso es puramente vertical (respecto a la superficie terrestre) mientras que la reacción del suelo, <math>\vec{\phi}</math>, cuando no hay rozamiento, es perpendicular a éste y por tanto forma un ángulo con la dirección del peso. Este ángulo es igual a la inclinación del peralte, <math>\alpha</math>. En forma vectorial | El peso es puramente vertical (respecto a la superficie terrestre) mientras que la reacción del suelo, <math>\vec{\phi}</math>, cuando no hay rozamiento, es perpendicular a éste y por tanto forma un ángulo con la dirección del peso. Este ángulo es igual a la inclinación del peralte, <math>\alpha</math>. En forma vectorial | ||
| - | <center><math>\vec{\ | + | <center><math>\vec{\Phi} = -\Phi\,\mathrm{sen}(\alpha)\vec{u}_\rho + \Phi\cos(\alpha)\vec{u}_z</math></center> |
Si separamos en componentes la segunda ley de Newton nos quedan las ecuaciones escalares | Si separamos en componentes la segunda ley de Newton nos quedan las ecuaciones escalares | ||
| - | <center><math>\begin{array}{rcl}\Phi\ | + | <center><math>\begin{array}{rcl}\Phi\,\mathrm{sen}(\alpha) & = & \displaystyle m\frac{|\vec{v}|^2}{R}\\ && \\ -mg + \Phi\cos(\alpha) & = & 0 \end{array} </math></center> |
| - | + | Despejando y dividiendo una por la otra queda la ecuación básica del peralte | |
| + | <center><math>\frac{|\vec{v}|^2}{Rg}=\mathrm{tg}(\alpha)</math></center> | ||
| + | |||
| + | lo que nos da la velocidad | ||
| + | |||
| + | <center><math>|\vec{v}| = \sqrt{Rg\,\mathrm{tg}(\alpha)}</math></center> | ||
| + | |||
| + | Sustituyendo los datos numéricos | ||
| + | |||
| + | <center><math>|\vec{v}| = \sqrt{(200\,\mathrm{m})\left(9.81\,\frac{\mathrm{m}}{\mathrm{s}^2}\right)\mathrm{tg}(9.2^\circ)} = 17.8\,\frac{\mathrm{m}}{\mathrm{s}} = 64.2\,\frac{\mathrm{km}}{\mathrm{h}}}</math></center> | ||
==Con rozamiento== | ==Con rozamiento== | ||
[[Categoría:Dinámica de la partícula (GIE)]] | [[Categoría:Dinámica de la partícula (GIE)]] | ||
Revisión de 19:24 12 sep 2011
1 Enunciado
El circuito de Indianápolis posee curvas de 200m de radio peraltadas un ángulo de 9º12'.
- Si no se considera el rozamiento, ¿con qué rapidez debe ir un coche si no quiere deslizarse ni hacia arriba ni hacia abajo?
- El coeficiente de rozamiento lateral de un coche con la pista vale μ = 1.5. ¿Cuáles son las velocidades máximas y mínimas que puede adquirir un coche sin derrapar?
2 Sin rozamiento
En la curva, el coche realiza un movimiento circular uniforme. La aceleración de este movimiento es puramente normal. De acuerdo con la segunda ley de Newton nos queda
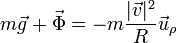
siendo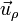 
el vector unitario radial hacia afuera. El signo menos viene de que la aceleración normal es siempre hacia adentro de la curva.
El peso es puramente vertical (respecto a la superficie terrestre) mientras que la reacción del suelo,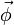 
, cuando no hay rozamiento, es perpendicular a éste y por tanto forma un ángulo con la dirección del peso. Este ángulo es igual a la inclinación del peralte, α. En forma vectorial
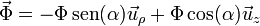
Si separamos en componentes la segunda ley de Newton nos quedan las ecuaciones escalares
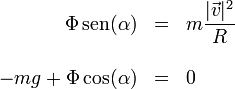
Despejando y dividiendo una por la otra queda la ecuación básica del peralte
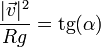
lo que nos da la velocidad
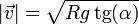
Sustituyendo los datos numéricos
