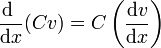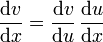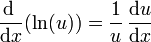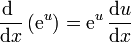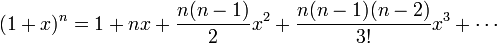Tabla de derivadas y primitivas
De Laplace
(Diferencias entre revisiones)
(→Series de Taylor) |
(→Series de Taylor) |
||
| Línea 106: | Línea 106: | ||
==Series de Taylor== | ==Series de Taylor== | ||
| + | |||
| + | :<math>(1+x)^n = 1 + n x + \frac{n(n-1)}{2}x^2+\frac{n(n-1)(n-2)}{3!}x^3+ \cdots</math> | ||
:<math>\frac{1}{1-x}=1+x+x^2+x^3+\cdots = \sum_{n=0}^\infty x^n</math> | :<math>\frac{1}{1-x}=1+x+x^2+x^3+\cdots = \sum_{n=0}^\infty x^n</math> | ||
Revisión de 16:55 30 ago 2011
Contenido |
1 Reglas de derivación
- Suma de funciones
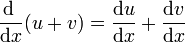
- Producto de funciones
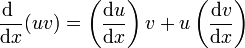
Caso particular u = C = cte
- Regla de la cadena
Caso particular de derivada logarítmica
Caso particular de exponencial de una función
2 Tabla de derivadas
| f(x) | df / dx | f(x) | df / dx |
|---|---|---|---|

| 
| 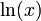
| 
|

| 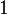
| 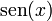
| 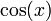
|
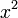
| 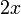
| 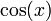
| 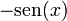
|

| 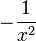
| 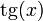
| 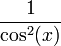
|
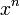
| 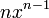
| 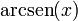
| 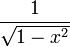
|
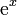
| 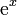
| 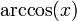
| 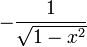
|

| 
| 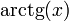
| 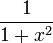
|
3 Tabla de primitivas
| f(x) | 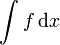
| f(x) | 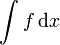
|
|---|---|---|---|

| 
| 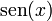
| 
|

| 
| 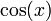
| 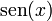
|

| 
| 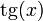
| 
|
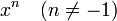
| 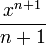
| 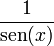
| 
|
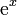
| 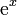
| 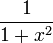
| 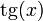
|
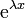
| 
| 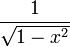
| 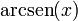
|
Más integrales en la Wikipedia