Tabla de derivadas y primitivas
De Laplace
(Diferencias entre revisiones)
(→Derivadas) |
(→Derivadas) |
||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Reglas de derivación== |
| + | ;Suma de funciones | ||
| + | :<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(u+v) = \frac{\mathrm{d}u}{\mathrm{d}x} + \frac{\mathrm{d}v}{\mathrm{d}x}</math> | ||
| + | |||
| + | ;Producto de funciones | ||
| + | :<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(uv) = \left(\frac{\mathrm{d}u}{\mathrm{d}x}\right)v + u\left(\frac{\mathrm{d}v}{\mathrm{d}x})</math> | ||
| + | |||
| + | Caso particular <math>u = C = \mathrm{cte}</math> | ||
| + | |||
| + | :<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(Cv) = C\left(\frac{\mathrm{d}v}{\mathrm{d}x})</math> | ||
| + | |||
| + | ;Regla de la cadena | ||
| + | |||
| + | :<math>\frac{\mathrm{d}u}{\mathrm{d}x}=\frac{\mathrm{d}u}{\mathrm{d}y}\,\frac{\mathrm{d}y}{\mathrm{d}x}</math> | ||
| + | |||
| + | :Caso particular de derivada logarítmica | ||
| + | :<math>\frac{\mathrm{d}\ }{\mathrm{d}x}(\ln(u)) = \frac{1}{u}\,\frac{\mathrm{d}u}{\mathrm{d}x}</math> | ||
| + | |||
| + | :Caso particular de exponencial de una función | ||
| + | :<math>\frac{\mathrm{d}\ }{\mathrm{d}x}\left(\mathrm{e}^u) = \mathrm{e}^u\,\frac{\mathrm{d}u}{\mathrm{d}x}</math> | ||
| + | |||
| + | ==Tabla de derivadas== | ||
{| class="bordeado" | {| class="bordeado" | ||
|- | |- | ||
Revisión de 16:33 30 ago 2011
1 Reglas de derivación
- Suma de funciones
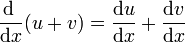
- Producto de funciones
- No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{\mathrm{d}\ }{\mathrm{d}x}(uv) = \left(\frac{\mathrm{d}u}{\mathrm{d}x}\right)v + u\left(\frac{\mathrm{d}v}{\mathrm{d}x})
Caso particular u = C = cte
- No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{\mathrm{d}\ }{\mathrm{d}x}(Cv) = C\left(\frac{\mathrm{d}v}{\mathrm{d}x})
- Regla de la cadena
- Caso particular de derivada logarítmica
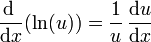
- Caso particular de exponencial de una función
- No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\mathrm{e}^u) = \mathrm{e}^u\,\frac{\mathrm{d}u}{\mathrm{d}x}
2 Tabla de derivadas
| f(x) | df / dx | f(x) | df / dx |
|---|---|---|---|

| 
| 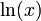
| 
|

| 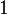
| 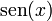
| 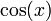
|
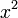
| 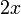
| 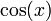
| 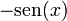
|

| 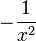
| 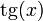
| 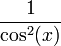
|
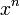
| 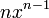
| 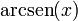
| 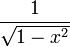
|
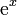
| 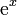
| 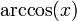
| 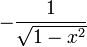
|

| 
| 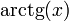
| 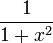
|






