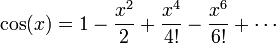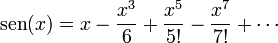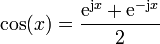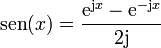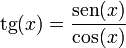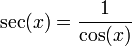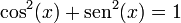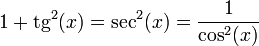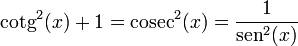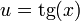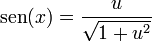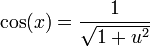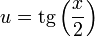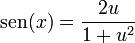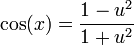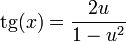Tabla de fórmulas de trigonometría
De Laplace
(Diferencias entre revisiones)
(→Tabla de valores particulares) |
(→Tabla de valores particulares) |
||
| Línea 96: | Línea 96: | ||
;Ángulo complementario | ;Ángulo complementario | ||
| - | <center><math>\mathrm{sen}\left(\frac{\pi}{2}-x)=\cos(x)\qquad \cos\left(\frac{\pi}{2}-x)=\mathrm{sen}(x)</math>{{qquad}}{{qquad}}<math>\mathrm{tg}\left(\frac{\pi}{2}-x)=\mathrm{cotg}(x)\qquad \mathrm{cotg}\left(\frac{\pi}{2}-x)=\mathrm{tg}(x)</math></center> | + | <center><math>\mathrm{sen}\left(\frac{\pi}{2}-x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}-x\right)=\mathrm{sen}(x)</math>{{qquad}}{{qquad}}<math>\mathrm{tg}\left(\frac{\pi}{2}-x\right)=\mathrm{cotg}(x)\qquad \mathrm{cotg}\left(\frac{\pi}{2}-x\right)=\mathrm{tg}(x)</math></center> |
==Suma y diferencia de ángulos== | ==Suma y diferencia de ángulos== | ||
Revisión de 21:12 28 ago 2011
Contenido |
1 Definiciones
1.1 Geométrica
1.2 Analítica
El argumento x debe estar expresado en radianes
1.3 Exponenciales complejas
(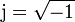 )
)
1.4 Funciones adicionales
2 Relaciones entre funciones
2.1 Identidades básicas
2.2 En función de la tangente
2.3 En función de la tangente del ángulo mitad
3 Tabla de valores particulares
| ° | rad | sen | cos | tg |
|---|---|---|---|---|
| 0 | 0 | 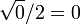
| 1 | 0 |
| 30 | π / 6 | 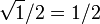
| 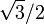
| 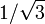
|
| 45 | π / 4 | 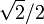
| 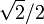
| 1 |
| 60 | π / 3 | 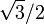
| 1 / 2 | 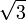
|
| 90 | π / 2 | 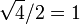
| 0 | 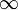
|
- Ángulo complementario