Bases vectoriales
De Laplace
(→Construcción de las bases) |
(→Construcción de las bases) |
||
| Línea 17: | Línea 17: | ||
Esto es, para cada punto, tomamos la línea coordenada <math>q_1\,</math>. Hallamos un vector tangente a ella, lo cual se puede hacer mediante la derivada | Esto es, para cada punto, tomamos la línea coordenada <math>q_1\,</math>. Hallamos un vector tangente a ella, lo cual se puede hacer mediante la derivada | ||
| - | <center><math>\mathbf{e} | + | <center><math>\mathbf{e}_i=\frac{\partial\mathbf{r}}{\partial q_i}</math></center> |
Este vector es tangente a la curva y apunta en el sentido correcto (del mismo modo que la velocidad de un movimiento <math>\mathbf{v} = \mathrm{d}(\mathbf{r})/\mathrm{d}t</math> es tangente a la trayectoria y apunta hacia adelante). Para obtener el vector unitario, calculamos el módulo de este vector y dividimos por él | Este vector es tangente a la curva y apunta en el sentido correcto (del mismo modo que la velocidad de un movimiento <math>\mathbf{v} = \mathrm{d}(\mathbf{r})/\mathrm{d}t</math> es tangente a la trayectoria y apunta hacia adelante). Para obtener el vector unitario, calculamos el módulo de este vector y dividimos por él | ||
| - | <center><math>h_1 = \left|\ | + | <center><math>h_1 = \left|\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}q_1}\right| \qquad\mathbf{u}_1=\frac{\mathbf{e}_1}{h_1}</math></center> |
De manera análoga construimos los vectores <math>\mathbf{u}_{2}\,</math>$ y <math>\mathbf{u}_{3}\,</math>. | De manera análoga construimos los vectores <math>\mathbf{u}_{2}\,</math>$ y <math>\mathbf{u}_{3}\,</math>. | ||
Revisión de 17:07 20 nov 2007
Contenido |
1 Introducción
La definición de sistemas de coordenadas está muy bien, y es muy útil, pero, por desgracia, no es suficiente. Dado que vamos a hablar de forma insistente de magnitudes vectoriales, vamos a necesitar expresar vectores en diferentes sistemas de coordenadas. Para ello necesitamos definir bases vectoriales, para poder escribir los vectores en términos de sus componentes. Por supuesto, una posibilidad sería definir una base de una vez por todas, por ejemplo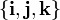 
, y expresar todos los vectores siempre en dicha base. Pero, aunque parece lo más cómodo, no es lo más sencillo. O, mejor dicho, no es esta base la que da una expresión más sencilla para los distintos vectores. Por ejemplo, El vector de posición en esféricas, empleando la base 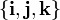se escribe
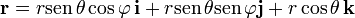
mientras que empleando la base específica de esféricas se escribe
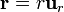
lo cual es mucho más sencillo, dónde va a parar... ¿o quizás no?
2 Construcción de las bases
Para los tres sistemas que hemos definido, podemos construir una base ortonormal en cada punto del espacio de la siguiente forma: Los vectores de la base en un punto 
son los vectores unitarios tangentes a las líneas coordenadas que pasan por dicho punto y en el sentido en el que aumenta cada coordenadas.
Esto es, para cada punto, tomamos la línea coordenada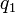 
. Hallamos un vector tangente a ella, lo cual se puede hacer mediante la derivada
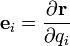
Este vector es tangente a la curva y apunta en el sentido correcto (del mismo modo que la velocidad de un movimiento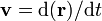 
es tangente a la trayectoria y apunta hacia adelante). Para obtener el vector unitario, calculamos el módulo de este vector y dividimos por él
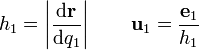
De manera análoga construimos los vectores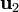 
$ y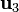 
.
Teniendo en cuenta que las líneas coordenadas son en general curvas,
con una dirección variable, se deduce la propiedad importante:
