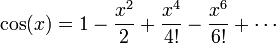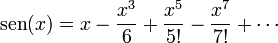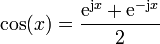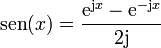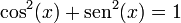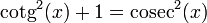Tabla de fórmulas de trigonometría
De Laplace
(Diferencias entre revisiones)
(→Identidades básicas) |
(→Identidades básicas) |
||
| Línea 29: | Línea 29: | ||
==Relaciones entre funciones== | ==Relaciones entre funciones== | ||
===Identidades básicas=== | ===Identidades básicas=== | ||
| - | + | #<math>\cos^2(x) + \mathrm{sen}^2(x) = 1\,</math> | |
| - | + | #<math>1 + \mathrm{tg}^2(x) = \mathrm{sec}^2(x)\,</math> | |
| - | + | #<math>\mathrm{cotg}^2(x) +1= \mathrm{cosec}^2(x)\,</math> | |
===En función del seno=== | ===En función del seno=== | ||
Revisión de 10:48 28 ago 2011
Contenido |
1 Definiciones
1.1 Geométrica
1.2 Analítica
El argumento x debe estar expresado en radianes
1.3 Exponenciales complejas
(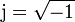 )
)