Derivación e integración en física (GIE)

De Laplace

(Diferencias entre revisiones)

Revisión de 17:33 24 ago 2011

Contenido

1 Introducción
2 Diferenciales
3 Derivadas
4 Integrales
5 Ecuaciones diferenciales

1 Introducción

El objeto de este tema no una exposición de las técnicas de derivación e integración, que se suponen conocidas. Se trata aquí de dar una interpretación intuitiva del significado de estas operaciones en física, a fin de facilitar tanto la compresión de las fórmulas como de saber cuándo y dónde deben utilizarse.

Lo que sigue no pretende en absoluto ser riguroso, es más, en muchos aspectos se aleja del rigor matemático, si con ello se consigue una mejor visualización del significado.

2 Diferenciales

La idea de diferencial es simple:

Un diferencial de una magnitud, $d A$ , es una cantidad muy pequeña de dicha magnitud

Por ejemplo, si estamos considerando el movimiento rectilíneo de una partícula, nos puede interesar el desplazamiento neto, $Δ x$ durante un periodo finito $Δ t$ . Pero si el movimiento es irregular, nos puede interesar un análisis más detallado del movimiento. En ese caso consideraríamos intervalos de tiempo muy cortos, en los cuales se realizan desplazamientos minúsculos. A esos intervalos, que serían instantes, los denotamos por $d t$ y a los desplazamientos pequeños por $d x$ y los llamamos diferenciales.

La pregunta que surge de manera inmediata es ¿cómo de pequeño? ¿pequeño comparado con qué? Una magnitud no es grande o pequeña en sentido absoluto; lo es siempre relativamente a alguna referencia.

A la hora de considerar una cantidad como diferencial, lo hacemos siempre comparándola con los valores típicos de las magnitudes que aparecen en el sistema que se está estudiando. Como criterio, podemos considerar que si es más de tres órdenes de magnitud más pequeño (menos de una milésima, preferible aun menor) se puede aproximar como diferencial. Por ejemplo, una distancia 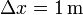$\Delta x = 1\,\mathrm{m}$ , ¿puede considerarse como diferencial? En un problema en el que estudiamos el movimiento de una pelota de ping-pong obviamente no. Pero, si lo que estamos estudiando es el movimiento de la Tierra alrededor del Sol, sí que se puede, muy justificadamente, considerar como diferencial.

Un diferencial no tiene por qué referirse al incremento de una variable.

En los casos $d t$ y $d x$ sí puede considerarse como incrementos muy pequeños en las variables $t$ y $x$ .

Supongamos ahora, que nos piden describir la temperatura de una habitación. Puesto que esta temperatura no será homogénea en general, no tiene mucho sentido hablar de la temperatura del conjunto. Es más lógico dividir la habitación en trozos lo suficientemente pequeños como para que cada uno tenga una temperatura concreta. Construimos así elementos de volumen $d V$ , que serían diferenciales, y a los cuales les podemos asignar una temperatura. Estos diferenciales de volumen no corresponden al incremento de ninguna variable. Se trata simplemente de cantidades muy pequeñas de una magnitud. Si nos imaginamos cada elemento de volumen como un pequeño cubito, su volumen sería largo por ancho por alto

$\mathrm{d}V = \mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z$

es decir, es el producto de tres diferenciales de variables diferentes.

También se pueden definir diferenciales de magnitudes vectoriales. Un desplazamiento en el espacio viene dado por el incremento del vector de posición

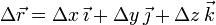
$\Delta\vec{r} = \Delta x\,\vec{\imath}+\Delta y\,\vec{\jmath}+\Delta z\,\vec{k}$

Si consideramos un desplazamiento muy pequeño comparado con el tamaño del sistema obtenemos un diferencial de camino

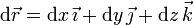
$\mathrm{d}\vec{r} = \mathrm{d} x\,\vec{\imath}+\mathrm{d} y\,\vec{\jmath}+\mathrm{d} z\,\vec{k}$

que, de nuevo, es una combinación de los incrementos infinitesimales de tres variables diferentes.

El tamaño de los diferenciales reales, en física, no puede hacerse infinitamente pequeño como en matemáticas. Imaginemos que estudiamos la distribución de temperatura en un baño de agua. Dividimos el agua el elementos de volumen de masa $d m$ . Si consideramos los elementos de volumen tendiendo a ser infinitamente pequeños, llega un momento en que dejan de ser volúmenes de agua, pasando a ser protones, electrones o espacio vacío, para los cuales la temperatura o el propio concepto de agua deja de tener sentido. Por ello, hemos de considerar que un diferencial es una cantidad mucho más pequeña que los valores que aparecen en el problema, pero no tan pequeña que dejen de tener significado.

Cuando tenemos una función de una o varias variables 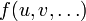$f(u, v,\ldots)$ y las variables cambian en una cantidad diferencial, el valor de la función $f$ también cambia de manera diferencial

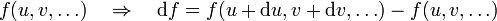
$f(u,v,\ldots) \quad\Rightarrow\quad \mathrm{d}f = f(u+\mathrm{d}u,v+\mathrm{d}v,\ldots)-f(u,v,\ldots)$

Así obtenemos la regla de que la diferencial de una suma es la suma de diferenciales

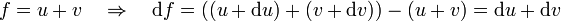
$f = u +v \quad\Rightarrow\quad \mathrm{d}f = ((u+\mathrm{d}u) +(v+\mathrm{d}v))-(u+v) = \mathrm{d}u+\mathrm{d}v$

En el caso de un producto obtenemos

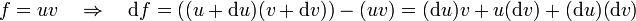
$f = uv \quad\Rightarrow\quad \mathrm{d}f = ((u+\mathrm{d}u)(v+\mathrm{d}v))-(uv) = (\mathrm{d}u)v+u(\mathrm{d}v)+(\mathrm{d}u)(\mathrm{d}v)$

pero en esta expresión, el último término es mucho más pequeño que los dos primeros. Imaginemos que u y v valen 1, y sus diferenciales valen 0.001, entonces, los dos primeros términos son del orden de la milésima, pero el tercero es del orden de una millonésima 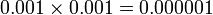$0.001\times 0.001 = 0.000001$ y por tanto es despreciable

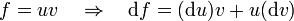
$f = uv \quad\Rightarrow\quad \mathrm{d}f = (\mathrm{d}u)v+u(\mathrm{d}v)$

Este ejemplo, nos muestra que existen categorías entre los diferenciales: de primer orden, de segundo orden -producto de dos-, de tercer orden -producto de tres-,… Cuando el resultado final de una operación es la suma de una cantidad finita con un diferencial, o un diferencial con un diferencial de orden superior, los términos más pequeños son despreciables, quedándonos siempre con el del orden más bajo.

En cuanto a las dimensiones y unidades, el diferencial de una magnitud tiene las mismas que la propia magnitud. Un diferencial de masa, $d m$ se mide en kilogramos y uno de tiempo, $d t$ en segundos.

3 Derivadas

El concepto básico de derivada es el siguiente:

Una derivada es un cociente entre dos cantidades muy pequeñas

El ejemplo más claro para ilustrarlo es el de velocidad instantánea. Cuando decimos que en un instante dado la velocidad es de 120 km/h, ¿qué estamos diciendo exactamente? Evidentemente, no que durante la última hora se han recorrido 120 km, ya que igual sólo se llevan 10 minutos de marcha. Podríamos decir que durante el último minuto se han recorrido 2 km. ya que

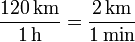
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}$

Esto ya es más preciso, pero aun no es del todo satisfactorio, ya que en un minuto hay tiempo suficiente a acelerar o frenar. Una mejor aproximación sería afirmar que en el último segundo se ha recorrido (1/30) km = 33.3 m. O podríamos decir que en la última décima de segundo se han recorrido 3.33 m,…

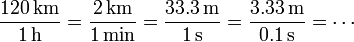
$\frac{120\,\mathrm{km}}{1\,\mathrm{h}} = \frac{2\,\mathrm{km}}{1\,\mathrm{min}}= \frac{33.3\,\mathrm{m}}{1\,\mathrm{s}}=\frac{3.33\,\mathrm{m}}{0.1\,\mathrm{s}}=\cdots$

En todos los casos la velocidad es de 120 km/h, pero cuanto más pequeño es el intervalo de tiempo considerado, más nos acercamos al ideal de medir la velocidad en un instante dado.

Se define entonces la velocidad instantánea como el cociente entre la distancia recorrida y el tiempo empleado en recorrerla, cuando ambas cantidades se hacen muy pequeñas, reduciéndose a diferenciales

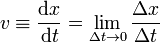
$v\equiv\frac{\mathrm{d}x}{\mathrm{d}t}=\lim_{\Delta t\to 0}\frac{\Delta x}{\Delta t}$

Este concepto se generaliza a toda derivada de una función f respecto a una variable u: El cociente entre el diferencial de la función y el de la variable

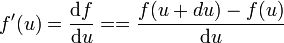
$f'(u) = \frac{\mathrm{d}f}{\mathrm{d}u} = = \frac{f(u+du)-f(u)}{\mathrm{d}u}$

Vemos que en una derivada tan importante es qué se deriva como con respecto a qué se deriva, ya que una misma magnitud puede depender de muchas otras (una fuerza puede depender del tiempo o de la posición; la energía de la presión, volumen o temperatura). Por tanto, en física no tiene mucho sentido hablar de “la derivada de la magnitud A”. Será siempre “la derivada de la magnitud $A$ respecto a la magnitud $x$ ”. Por ello, es siempre preferible usar la notación de Leibniz, como el cociente entre diferenciales $d A / d x$ .

De la definición de derivada como cociente de diferenciales se deduce que las dimensiones de una derivada son las del numerador (la magnitud que se deriva) dividida por la del denominador (respecto a qué se deriva). Así, para la velocidad instantánea, cociente entre un diferencial de posición y uno de tiempo, las dimensiones son L/T.

Geométricamente, la derivada de una magnitud, A, respecto a otra, x, se obtiene representando A frente a x. Si consideramos dos puntos de la curva, la pendiente de la recta que pasa por esos dos puntos vale

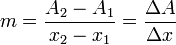
$m = \frac{A_2-A_1}{x_2-x_1} = \frac{\Delta A}{\Delta x}$

Considerando ahora intervalos cada vez más pequeños, la recta secante tiende a convertirse en la recta tangente y la pendiente de la recta tangente equivale a la derivada $d A / d x$ .

Esta interpretación se relaciona con una aplicación muy importante de las derivadas: la aproximación lineal. Si tenemos una magnitud dependiente de otra de una forma suave, de forma que alrededor de un cierto punto no hay un cambio sustancial de dirección, podemos hacer la aproximación de que para puntos próximos

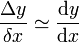
$\frac{\Delta y}{\delta x}\simeq \frac{\mathrm{d}y}{\mathrm{d}x}$

o, equivalentemente

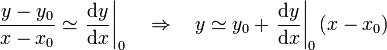
$\frac{y-y_0}{x-x_0}\simeq \left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_0\quad\Rightarrow\quad y \simeq y_0+\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_0(x-x_0)$

Esta es justamente la ecuación de la recta tangente a la curva en $x = x 0$ , entonces, la aproximación lineal consiste en sustituir la función por la recta tangente. Por supuesto, esto solo es una aproximación válida en puntos próximos al de tangencia.

Así, por ejemplo, para un resorte, tenemos que cuando su longitud es la de reposo, $l 0$ , no ejerce fuerza alguna, pero si estiramos o comprimimos el resorte aparece una fuerza en sentido opuesto

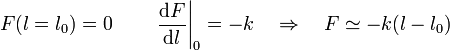
$F(l=l_0) = 0\qquad \left.\frac{\mathrm{d}F}{\mathrm{d}l}\right|_0 = -k \quad \Rightarrow \quad F\simeq -k(l-l_0)$

Esta es la ley de Hooke, que solo es válida cuando la deformación del muelles es pequeña. Para deformaciones grandes, la ley deja de ser cierta.

A partir de las expresiones para los diferenciales de una suma y de un producto obtenemos las de la derivada de una suma y un producto, simplemente operando como si fueran fracciones (que es lo que son)

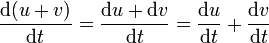
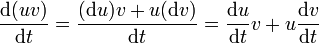
$\frac{\mathrm{d}(u+v)}{\mathrm{d}t}=\frac{\mathrm{d}u+\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}u}{\mathrm{d}t}+\frac{\mathrm{d}v}{\mathrm{d}t}$ $\frac{\mathrm{d}(uv)}{\mathrm{d}t}=\frac{(\mathrm{d}u)v+u(\mathrm{d}v)}{\mathrm{d}t}=\frac{\mathrm{d}u}{\mathrm{d}t}v+u\frac{\mathrm{d}v}{\mathrm{d}t}$

La derivación puede extenderse al caso de una magnitud vectorial respecto a una escalar. Algebráicamente equivale a multiplicar el vector 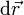$\mathrm{d}\vec{r}$ por el escalar $1 / d t$ ,

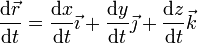
$\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}x}{\mathrm{d}t}\vec{\imath}+\frac{\mathrm{d}y}{\mathrm{d}t}\vec{\jmath}+\frac{\mathrm{d}z}{\mathrm{d}t}\vec{k}$

pero NO se puede extender a la derivada respecto a una magnitud vectorial, ya que ello implicaría dividir por un vector, lo que no es admisible.

4 Integrales

5 Ecuaciones diferenciales

@@ Línea 111: / Línea 111: @@
 <center><math>\frac{\mathrm{d}(u+v)}{\mathrm{d}t}=\frac{\mathrm{d}u+\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}u}{\mathrm{d}t}+\frac{\mathrm{d}v}{\mathrm{d}t}</math>{{qquad}}{{qquad}}<math>\frac{\mathrm{d}(uv)}{\mathrm{d}t}=\frac{(\mathrm{d}u)v+u(\mathrm{d}v)}{\mathrm{d}t}=\frac{\mathrm{d}u}{\mathrm{d}t}v+u\frac{\mathrm{d}v}{\mathrm{d}t}</math></center>
+La derivación puede extenderse al caso de una magnitud vectorial respecto a una escalar. Algebráicamente equivale a multiplicar el vector <math>\mathrm{d}\vec{r}</math> por el escalar <math>1/\mathrm{d}t</math>,
+<center><math>\frac{\mathrm{d}\vec{r}}{\mathrm{d}t} = \frac{\mathrm{d}x}{\mathrm{d}t}\vec{\imath}+\frac{\mathrm{d}y}{\mathrm{d}t}\vec{\jmath}+\frac{\mathrm{d}z}{\mathrm{d}t}\vec{k}</math></center>
+pero NO se puede extender a la derivada respecto a una magnitud vectorial, ya que ello implicaría dividir por un vector, lo que no es admisible.
 ==Integrales==
 ==Ecuaciones diferenciales==
 [[Categoría:Herramientas matemáticas (GIE)]]

Derivación e integración en física (GIE)

De Laplace

Revisión de 17:33 24 ago 2011

Contenido

1 Introducción

2 Diferenciales

3 Derivadas

4 Integrales

5 Ecuaciones diferenciales

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES