Vectores en física (GIE)
De Laplace
(→Tipos de magnitudes) |
(→Operaciones con vectores) |
||
| Línea 74: | Línea 74: | ||
<center><math>\left|\vec{r}\times\vec{F}\right| = \frac{1}{2}mv^2</math></center> | <center><math>\left|\vec{r}\times\vec{F}\right| = \frac{1}{2}mv^2</math></center> | ||
| - | ==Operaciones con | + | ==Operaciones con magnitudes escalares== |
| + | Las magnitudes escalares se comportan como números reales y por tanto admiten las operaciones básicas entre números: suma y multiplicación (con sus respectivas inversas y combinaciones entre ellas). | ||
| + | |||
| + | La suma de magnitudes escalares debe respetar el principio de homogeneidad dimensional, esto es, las magnitudes sumadas deben poseer las mismas dimensiones (no se puede sumar una distancia a un tiempo). | ||
| + | |||
| + | En el producto de magnitudes escalares, el resultado tiene por dimensiones el producto de las dimensiones de los diferentes factores. Así, por ejemplo la densidad de masa | ||
| + | |||
| + | <center><math>\rho = \frac{m}{V}</math></center> | ||
| + | |||
| + | pose dimensiones | ||
| + | |||
| + | <center><math>[\rho]=\frac{[m]}{[V]} = \frac{M}{L^3}= M\cdot L^{-3}</math></center> | ||
| + | |||
| + | y se medirá en el SI en kg/m³. | ||
| + | |||
| + | ==Operaciones con magnitudes vectoriales== | ||
===Suma de vectores=== | ===Suma de vectores=== | ||
===Producto por un escalar=== | ===Producto por un escalar=== | ||
===Producto escalar=== | ===Producto escalar=== | ||
===Producto vectorial=== | ===Producto vectorial=== | ||
| + | |||
==Sistemas de referencia== | ==Sistemas de referencia== | ||
===Ejes=== | ===Ejes=== | ||
Revisión de 11:17 6 ago 2011
Contenido |
1 Magnitudes escalares y vectoriales
2 Tipos de magnitudes
Una magnitud física es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (t), la velocidad
( ), la masa (m), la temperatura (T), el campo eléctrico (
), la masa (m), la temperatura (T), el campo eléctrico (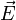 ).
).
Las magnitudes físicas se pueden clasificar en:
- Magnitudes escalares
- Las magnitudes escalares son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales). Así, por ejemplo, si decimos que la masa de un objeto es 3 kg, hemos aportado toda la información necesaria.
- Magnitudes vectoriales
- Las magnitudes vectoriales son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación y su punto de aplicación. Así, al decir que sobre un objeto se aplica una fuerza de 3 N, no poseemos toda la información, ya que habrá que indicar hacia dónde se dirige dicha fuerza.
| Ejemplos de magnitudes | |||
|---|---|---|---|
| Escalares | Vectoriales | ||
| Magnitud | Símbolo | Magnitud | Símbolo |
| Masa | m | Posición | 
|
| Tiempo | t | Velocidad | 
|
| Temperatura | T | Fuerza | 
|
| Energía | E | Campo eléctrico | 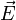
|
Obsérvese la diferencia en la notación entre magnitudes escalares y vectoriales. Por la condición de la homogeneidad que se comenta más abajo, es muy importante tener claro e indicar qué magnitud es escalar y cuál vectorial. Por ello, adoptaremos el convenio de siempre escribir las magnitudes vectoriales con flecha (también es admisible el usar negrita)
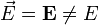
Además de las magnitudes escalares y vectoriales, existen otros tipos de magnitudes “de orden superior”, conocidas en general como magnitudes tensoriales.
Una magnitud escalar se puede representar por un número (con unidades), lo que equivale a una matriz 1×1. Una magnitud vectorial puede ser representadas por una vector fila o uno columna, que equivale a una matriz 1×3 o 3×1. Una magnitud tensorial requiere matrices 3×3 o incluso entes de mayores dimensiones.
Un ejemplo de magnitud tensorial son los “esfuerzos” en un sólido. Cuando se aplica una fuerza en una dirección resulta una deformación que puede ir en una dirección diferente. Por tanto necesitamos la información de la dirección y sentido de los dos, fuerza y deformación, por lo que no nos basta con una magnitud vectorial.
En este curso las magnitudes tensoriales aparecen muy raramente.
2.1 Principio de homogeneidad
Una propiedad importante de las leyes físicas es que son homogéneas. Esto quiere decir que los dos miembros de una igualdad, o cada uno de los sumandos de una suma, deben ser del mismo tipo:
- Una cantidad escalar será igual a otra cantidad escalar, por ejemplo
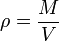
- Una cantidad vectorial será igual a otra cantidad vectorial
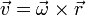
- pero nunca una cantidad escalar será igual a una vectorial. Por ejemplo, el momento de una fuerza es una cantidad cuya unidad SI es 1 N·m, y la energía cinética es una magnitud cuya unidad es 1 J = 1 N·m, pero aunque se miden en las mismas unidades, el momento de una fuerza nunca puede ser igual a la energía cinética, pues la primera es una magnitud vectorial y la segunda es una escalar
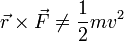
La energía cinética sí podrá ser igual al módulo del momento de la fuerza, que es una cantidad escalar
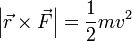
3 Operaciones con magnitudes escalares
Las magnitudes escalares se comportan como números reales y por tanto admiten las operaciones básicas entre números: suma y multiplicación (con sus respectivas inversas y combinaciones entre ellas).
La suma de magnitudes escalares debe respetar el principio de homogeneidad dimensional, esto es, las magnitudes sumadas deben poseer las mismas dimensiones (no se puede sumar una distancia a un tiempo).
En el producto de magnitudes escalares, el resultado tiene por dimensiones el producto de las dimensiones de los diferentes factores. Así, por ejemplo la densidad de masa
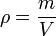
pose dimensiones
![[\rho]=\frac{[m]}{[V]} = \frac{M}{L^3}= M\cdot L^{-3}](/wiki/images/math/5/0/a/50a9d76bc3b716c1dd3f15333406f4d5.png)
y se medirá en el SI en kg/m³.





