Espira con barra deslizante y generador real

De Laplace

Revisión de 12:26 24 jun 2011 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) ← Edición más antigua		Revisión de 12:26 24 jun 2011 (ver código fuente) Gabriel (Discusión | contribuciones) (→Solución) Edición más nueva →
Línea 14:		Línea 14:
	\mathbf{u}_z</math></center>		\mathbf{u}_z</math></center>
-	En el enunciado se indica que tanto <math>B_0</math> como <math>v</math>, van a ser valores constantes. Por otra parte, podemos considerar sin pérdida de generalidad que <math>B_0</math> es una cantidad positiva (el sentido del eje <math>OX</math> es el del campo magnético); sin embargo, la ''celeridad'' <math>\displaystyle v</math> va a ser es un número real cuyo signo indica el sentido de movimiento de la barra conductora.	+	En el enunciado se indica que tanto <math>\displaystyle B_0</math> como <math>\displaystyle v</math>, van a ser valores constantes. Por otra parte, podemos considerar sin pérdida de generalidad que <math>\displaystyle B_0</math> es una cantidad positiva (el sentido del eje <math>OX</math> es el del campo magnético); sin embargo, la ''celeridad'' <math>\displaystyle v</math> va a ser es un número real cuyo signo indica el sentido de movimiento de la barra conductora.
	===Fuerzas electromotrices e intensisades de corriente===		===Fuerzas electromotrices e intensisades de corriente===

---

Revisión de 12:26 24 jun 2011

1 Enunciado

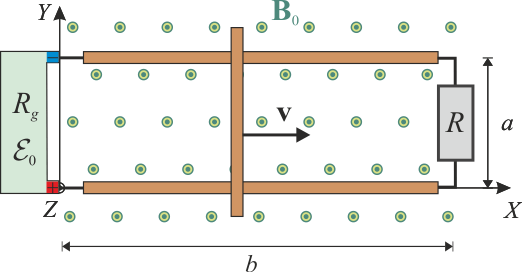
Una espira plana rectangular de autoinducción despreciable está formada por dos raíles perfectamente conductores de longitud b, separados una distancia a. Los raíles están conectados por uno de sus extremos a una resistencia eléctrica de valor R (resistencia de carga) y por el otro a un generador real de fuerza electromotriz constante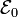 y resistencia interna R_g, según se muestra en la figura. Además, una barra perfectamente conductora se mueve con velocidad constante , manteniéndose siempre en contacto con los raíles y perpendicular a ellos. La espira se encuentra sometida a un campo magnético constante y uniforme , perpendicular al plano que contiene a la espira.

1. Obtenga las fuerzas electromotrices totales en cada malla del circuito y las intensidades de corriente eléctrica que recorren las diferentes ramas.
2. Calcule la fuerza magnética ejercida sobre la barra móvil, así como la fuerza exterior que se la ha de aplicar para que se mueva según las condiciones del enunciado. Describa la dependencia del sentido de esta fuerza con la velocidad y el sentido de movimiento de la barra.
3. Realice un balance energético en el sistema: calcule la potencia disipada por efecto Joule en la resistencia de carga, la potencia suministrada por el generador real al resto del sistema y el trabajo que por unidad de tiempo realiza la fuerza externa (potencia mecánica).
4. La potencia eléctrica suministrada por el generador real y la potencia mecánica realizada por la fuerza exterior, ¿son siempre positivas? Analice cómo depende el signo de éstas de la rapidez y sentido de movimiento de la barra y explique en cada caso dónde se produce y dónde se absorbe la energía en el sistema.

2 Solución

Adoptamos un sistema de referencia cartesiano cuyas direcciones X y Z van a estar definidas, respectivamente, por la dirección de movimiento de la barra conductora y por la dirección del campo magnético uniforme. Es decir,

En el enunciado se indica que tant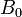o como 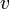, van a ser valores constantes. Por otra parte, podemos considerar sin pérdida de generalidad que 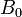es una cantidad positiva (el sentido del eje OX es el del campo magnético); sin embargo, la celeridad 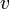va a ser es un número real cuyo signo indica el sentido de movimiento de la barra conductora.

2.1 Fuerzas electromotrices e intensisades de corriente