Campo de un tubo cilíndrico

De Laplace

(Diferencias entre revisiones)

Revisión de 20:24 30 may 2011

Contenido

1 Enunciado
2 Introducción
3 En forma integral
4 En forma diferencial

1 Enunciado

Sobre un cilindro de radio $a$ y longitud infinita fluye una corriente superficial de densidad uniforme 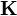$\mathbf{K}$ . Halle el campo magnético en todos los puntos del espacio.

2 Introducción

Aunque el enunciado no dice explícitamente hacia dónde se dirige la corriente, si esta es uniforme, no puede ser otra que

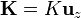
$\mathbf{K}=K\mathbf{u}_{z}\,$

Si supusiéramos, por ejemplo, una corriente 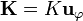$\mathbf{K}=K\mathbf{u}_{\varphi}$ no sería uniforme, pues 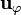$\mathbf{u}_{\varphi}$ depende de la posición.

El problema puede resolverse empleando las ecuaciones de la magnetostática en forma diferencial y en forma integral.

3 En forma integral

4 En forma diferencial

En forma diferencial debemos resolver las ecuaciones de la magnetostática

$\begin{array}{rcl} \nabla\cdot\mathbf{B} & = & 0 \\ && \\ \nabla\times\mathbf{B} & = & \mu_0\mathbf{J}=\mathbf{0} \end{array}$

junto con las correspondientes condiciones de salto en la superficie del cilindro:

$\begin{array}{rcl} \mathbf{n}\cdot[\mathbf{B}] & = & 0 \\ && \\ \mathbf{n}\times[\mathbf{B}] & = & \mu_0\mathbf{K} \end{array}$

Además, debemos tener en cuenta que el campo magnético sólo se puede hacer infinito en puntos donde haya distribuciones de corriente lineales, nunca donde no haya corriente. También que en puntos alejados del cilindro el campo debe anularse.

Tenemos que, como en el caso del cable grueso, existe simetría traslacional y rotacional. Por ello, ninguna de las tres componentes depende de $z$ ni de $\varphi$ .

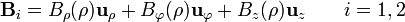
$\mathbf{B}_i = B_\rho(\rho)\mathbf{u}_\rho+B_\varphi(\rho)\mathbf{u}_\varphi+B_z(\rho)\mathbf{u}_z\qquad i = 1,2$

donde denominamos región 1 al interior del tubo y región 2 al exterior.

Aplicando la ley de Gauss para el campo magnético resulta

$0 = \nabla\cdot\mathbf{B} = \frac{1}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(\rho B_\rho\right)\quad\Rightarrow\quad B_\rho = \frac{k_i}{\rho}$

siendo $k i$ dos constantes, una para el interior del tubo y otra para el exterior

Ahora bien, puesto que el campo no puede tender a 0 en $ρ = 0$ , ya que el campo no puede diverger donde no hay corrientes, resulta que

$k_1 = 0\,$

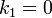
y aplicando ahora la condición de salto para la componente normal

$0 = \mathbf{n}\cdot[\mathbf{B}] = \mathbf{u}_\rho\cdot\left(\mathbf{B}_2(a^+)-\mathbf{B}_1(a^-)\right) = \frac{k_2}{a}-0\quad\Rightarrow\quad k_2 = 0$

y por tanto, como consecuencia de la ley de Gauss para el campo magnético, la componente radial es nula en todo el espacio.

$B_\rho=0\,$

Aplicando ahora la ley de Ampère en cada región tenemos

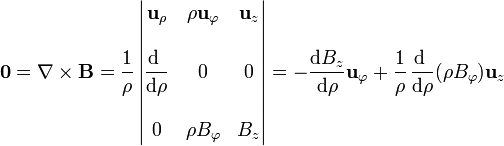
$\mathbf{0}=\nabla\times\mathbf{B}=\frac{1}{\rho}\left|\begin{matrix}\mathbf{u}_\rho & \rho\mathbf{u}_\varphi & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\mathrm{d}\ }{\mathrm{d}\rho} & 0 & 0 \\ & & \\ 0 & \rho B_\varphi & B_z\end{matrix}\right| = -\frac{\mathrm{d}B_z}{\mathrm{d}\rho}\mathbf{u}_\varphi + \frac{1}{\rho}\,\frac{\mathrm{d}\ }{\mathrm{d}\rho}(\rho B_\varphi)\mathbf{u}_z$

Un vector es nulo cuando son nulas cada una de sus componentes. Por ello, las componentes en el interior y el exterior pueden escribirse como

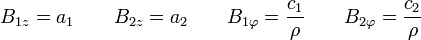
$B_{1z}=a_1\qquad B_{2z}=a_2\qquad B_{1\varphi}=\frac{c_1}{\rho}\qquad B_{2\varphi}=\frac{c_2}{\rho}$

La condición de que el campo no sea singular en el eje significa

$c_1=0\,$

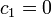
mientras que la anulación del campo en el infinito supone

$a_2=0\,$

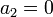
Las otras dos constantes se obtienen de la condición de salto, que en este caso es

$\mathbf{n}\times[\mathbf{B}]=a_1\mathbf{u}_{\varphi}+\frac{k_2}{R}\mathbf{u}_{z}=\mu_0\mathbf{K}=\mu_0 K\mathbf{u}_{z} \quad\Rightarrow\quad a_1=0\qquad k_2=\mu_0 K a$

con lo que el resultado final es que el campo se anula en el interior

$\mathbf{B}_1=0\,$

y en el exterior decae como la inversa de la distancia al eje

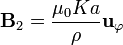
$\mathbf{B}_2=\frac{\mu_0 K a}{\rho}\mathbf{u}_{\varphi}$

Este campo exterior es idéntico al de un hilo de corriente cuya intensidad es

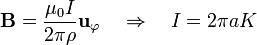
$\mathbf{B}=\frac{\mu_0I}{2\pi\rho}\mathbf{u}_{\varphi}\quad\Rightarrow\quad I=2\pi a K$

Esta corriente es justamente la cantidad total que fluye a través de una sección del tubo de corriente. Resulta entonces que el campo debido a un tubo hueco por el cual circula una corriente longitudinal, es nulo en el exterior y en el interior es el mismo que habría si toda la corriente circulara por el centro del tubo.

Campo de un tubo cilíndrico

De Laplace

Revisión de 20:24 30 may 2011

Contenido

1 Enunciado

2 Introducción

3 En forma integral

4 En forma diferencial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

@@ Línea 15: / Línea 15: @@
 En forma diferencial debemos resolver las ecuaciones de la magnetostática
-<center><math>\begin{array}{lcr}
+<center><math>\begin{array}{rcl}
 \nabla\cdot\mathbf{B} & = & 0 \\ && \\
 \nabla\times\mathbf{B} & = & \mu_0\mathbf{J}=\mathbf{0}
@@ Línea 22: / Línea 22: @@
 junto con las correspondientes condiciones de salto en la superficie del cilindro:
-<center><math>\begin{array}{lcr}
+<center><math>\begin{array}{rcl}
 \mathbf{n}\cdot[\mathbf{B}] & = & 0 \\ && \\
 \mathbf{n}\times[\mathbf{B}] & = & \mu_0\mathbf{K}