Entrar Página Discusión Historial Go to the site toolbox

Condensador relleno de un medio estratificado

De Laplace

(Diferencias entre revisiones)
(→Cálculo de los campos)
(→Cálculo de los campos)
Línea 39: Línea 39:
Tenemos que el campo eléctrico no depende de las coordenadas transversales, mientra que el desplazamiento no depende de la coordenada normal a las placas. Sin embargo, ¿depende el campo eléctrico de z? ¿Depende D de x e y? Para eso precisamos la relación constitutiva. Si derivamos el campo eléctrico respecto a z obtenemos
Tenemos que el campo eléctrico no depende de las coordenadas transversales, mientra que el desplazamiento no depende de la coordenada normal a las placas. Sin embargo, ¿depende el campo eléctrico de z? ¿Depende D de x e y? Para eso precisamos la relación constitutiva. Si derivamos el campo eléctrico respecto a z obtenemos
-
<center><math>\frac{\partial E}{\partial z} = \frac{\partial }{\partial z}\left(\frac{D}{\varepsilon(z)}\right) = \frac{1}{\varepsilon(z)}\overbrace{\frac{\partial D}{\partial z}}^{=0}-\frac{D}{\varepsilon^2}\frac{\mathrm{d} \varepsilon}{\mathrm{d} z}\neq 0</math></center>
+
<center><math>\frac{\partial E}{\partial z} = \frac{\partial }{\partial z}\left(\frac{D}{\varepsilon(z)}\right) = \frac{1}{\varepsilon}\overbrace{\frac{\partial D}{\partial z}}^{=0}-\frac{D}{\varepsilon^2}\overbrace{\frac{\partial \varepsilon}{\partial z}}^{\neq 0}\neq 0</math></center>
Esto es, en este sistema, el campo eléctrico no es uniforme entre las placas, sino que depende de la coordenada normal.
Esto es, en este sistema, el campo eléctrico no es uniforme entre las placas, sino que depende de la coordenada normal.
Línea 45: Línea 45:
El vector desplazamiento, en cambio, sí que es uniforme. Ya sabemos que no depende de z. Es fácil ver que tampoco depende ni de x
El vector desplazamiento, en cambio, sí que es uniforme. Ya sabemos que no depende de z. Es fácil ver que tampoco depende ni de x
-
<center><math>\frac{\partial D}{\partial x} = \frac{\partial }{\partial x}\left(\varepsilon(z)E\right) = \varepsilon(z)\overbrace{\frac{\partial E}{\partial x}}^{=0}+E\overbrace{\frac{\partial \varepsilon}{\partial x}}^{=0}= 0</math></center>
+
<center><math>\frac{\partial D}{\partial x} = \frac{\partial }{\partial x}\left(\varepsilon(z)E\right) = \varepsilon\overbrace{\frac{\partial E}{\partial x}}^{=0}+E\overbrace{\frac{\partial \varepsilon}{\partial x}}^{=0}= 0</math></center>
ni, análogamente, de y. Por tanto, podemos escribir
ni, análogamente, de y. Por tanto, podemos escribir

Revisión de 20:36 21 may 2011

Contenido

1 Enunciado

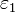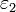Un medio estratificado es aquel cuyas propiedades dependen de la altura z. Un material de este tipo se coloca entre dos placas conductoras planas y paralelas, separadas una distancia a. La permitividad del material varía de \varepsilon_1 a \varepsilon_2 en la forma

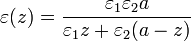
\varepsilon(z)= \frac{\varepsilon_1\varepsilon_2a}{\varepsilon_1z+\varepsilon_2(a-z)}

Si se aplica una diferencia de potencial V0 entre las placas,

  1. ¿Cuánto valen los campos \mathbf{D}, \mathbf{E} y \mathbf{P} en todos los puntos del material?
  2. ¿Cuál es la densidad de carga de polarización (tanto superficial como de volumen)?
  3. Halle la energía almacenada en el sistema

Desprecie los efectos de borde.

2 Cálculo de los campos

Por tratarse de una situación electrostática y no haber carga libre en el dieléctrico, por ser este ideal, se cumple

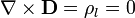
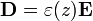
\nabla\times\mathbf{D}=\rho_l=0        \nabla\times\mathbf{E}=\mathbf{0}        \mathbf{D}=\varepsilon(z) \mathbf{E}

Si suponemos despreciables los efectos de borde y admitimos que los campos van en línea recta de una placa a la otra, escribimos el campo eléctrico y el vector desplazamiento como

\mathbf{E}=E\mathbf{u}_z\qquad\qquad\mathbf{D}=D\mathbf{u}_z

lo cual sustituyendo en las ecuaciones de la electrostática nos da, para la ley de Gauss

0 = \nabla\cdot\mathbf{D} = 0 + 0 + \frac{\partial D}{\partial z}

y para la irrotacionalidad del campo eléctrico

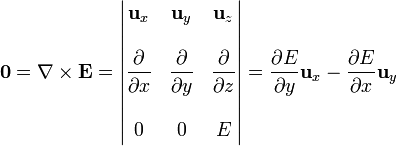
\mathbf{0}=\nabla\times\mathbf{E}=\left|\begin{matrix} \mathbf{u}_x & \mathbf{u}_y & \mathbf{u}_z \\ & & \\ \displaystyle\frac{\partial }{\partial x} & \displaystyle\frac{\partial }{\partial y} & \displaystyle\frac{\partial }{\partial z} \\ & & \\ 0 & 0 & E\end{matrix}\right| = \frac{\partial E}{\partial y}\mathbf{u}_x - \frac{\partial E}{\partial x} \mathbf{u}_y

puesto que un vector se anula cuando se anulan sus componentes, este sistema equivale a las ecuaciones

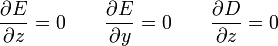
\frac{\partial E}{\partial z} = 0 \qquad \frac{\partial E}{\partial y} = 0 \qquad \frac{\partial D}{\partial z} = 0

Tenemos que el campo eléctrico no depende de las coordenadas transversales, mientra que el desplazamiento no depende de la coordenada normal a las placas. Sin embargo, ¿depende el campo eléctrico de z? ¿Depende D de x e y? Para eso precisamos la relación constitutiva. Si derivamos el campo eléctrico respecto a z obtenemos

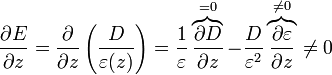
\frac{\partial E}{\partial z} = \frac{\partial }{\partial z}\left(\frac{D}{\varepsilon(z)}\right) = \frac{1}{\varepsilon}\overbrace{\frac{\partial D}{\partial z}}^{=0}-\frac{D}{\varepsilon^2}\overbrace{\frac{\partial \varepsilon}{\partial z}}^{\neq 0}\neq 0

Esto es, en este sistema, el campo eléctrico no es uniforme entre las placas, sino que depende de la coordenada normal.

El vector desplazamiento, en cambio, sí que es uniforme. Ya sabemos que no depende de z. Es fácil ver que tampoco depende ni de x

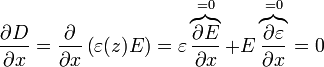
\frac{\partial D}{\partial x} = \frac{\partial }{\partial x}\left(\varepsilon(z)E\right) = \varepsilon\overbrace{\frac{\partial E}{\partial x}}^{=0}+E\overbrace{\frac{\partial \varepsilon}{\partial x}}^{=0}= 0

ni, análogamente, de y. Por tanto, podemos escribir

\mathbf{D}=D_0\mathbf{u}_z\qquad\qquad \mathbf{E}=\frac{D_0}{\varepsilon(z)}\mathbf{u}_z

siendo D0 una constante a determinar.

3 Densidades de carga

4 Energía almacenada

Obtenido de "http://tesla.us.es/wiki/index.php/Condensador_relleno_de_un_medio_estratificado"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace