Ecuaciones de Maxwell FII GIA
De Laplace
(Diferencias entre revisiones)
(→Introducción) |
(→Introducción) |
||
| Línea 11: | Línea 11: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | En esta ley se resumen varios datos sobre el campo eléctrico | ||
| + | #Las cargas eléctricas crean campo eléctrico. | ||
| + | #Las líneas de campo eléctrico mueren en las cargas positivas y mueren en las cargas negativas. | ||
| + | #El campo eléctrico se calcula a partir de la distribución de carga eléctrica. | ||
=== Ley de Gauss magnética === | === Ley de Gauss magnética === | ||
| Línea 19: | Línea 23: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | En esta ley se resumen varios datos sobre el campo magnético | ||
| + | #No existen cargas magnéticas. | ||
| + | #Las líneas de campo magnético son líneas cerradas. | ||
=== Ley de Faraday === | === Ley de Faraday === | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \oint\limits_{\Gamma}\vec{E}\cdot\mathrm{d}\vec{l} = -\dfrac{\mathrm{d}}{\mathrm{d}t} \int\limits_{S_{\Gamma}}\vec{B}\cdot\mathrm{d}\vec{A} | ||
| + | </math> | ||
| + | </center> | ||
| + | La letra <math>\Gamma </math> representa una línea cerrada, y <math>S_{\Gamma} </math> es una superficie apoyada en esa línea. | ||
| + | |||
| + | En esta ley se expresa el hecho de que un campo magnético variable en el tiempo es capaz de producir un campo eléctrico. Por tanto, hay dos fuentes de campo eléctrico: las cargas eléctricas y un campo magnético variable en el tiempo. | ||
=== Ley de Ampère === | === Ley de Ampère === | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \oint\limits_{\Gamma} \vec{B}\cdot\mathrm{d}\vec{l} | ||
| + | = | ||
| + | \mu_0\left.I\right|_{S_{\Gamma}} | ||
| + | </math> | ||
| + | </center> | ||
| + | Aquí, <math>\Gamma </math> representa una línea cerrada y <math>\left.I\right|_{S_{\Gamma}} </math> es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea <math>\Gamma </math>. | ||
| + | |||
| + | Esta ley nos dice que | ||
| + | #Las corrientes eléctricas generan campos magnéticos. | ||
| + | #Las líneas de campo magnético generado por estas corrientes dan vueltas alrededor de las corrientes. | ||
| + | #El campo magnético se puede calcular a partir de la distribución de corriente eléctrica. | ||
== Corriente de desplazamiento == | == Corriente de desplazamiento == | ||
Revisión de 09:32 3 may 2011
Contenido |
1 Introducción
Los fenómenos electromagnéticos que hemos visto hasta ahora se pueden explicar con cuatro leyes básicas. Estas leyes, en su expresión integral, son
1.1 Ley de Gauss
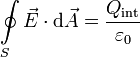
En esta ley se resumen varios datos sobre el campo eléctrico
- Las cargas eléctricas crean campo eléctrico.
- Las líneas de campo eléctrico mueren en las cargas positivas y mueren en las cargas negativas.
- El campo eléctrico se calcula a partir de la distribución de carga eléctrica.
1.2 Ley de Gauss magnética
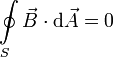
En esta ley se resumen varios datos sobre el campo magnético
- No existen cargas magnéticas.
- Las líneas de campo magnético son líneas cerradas.
1.3 Ley de Faraday
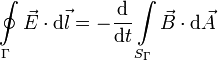
La letra Γ representa una línea cerrada, y SΓ es una superficie apoyada en esa línea.
En esta ley se expresa el hecho de que un campo magnético variable en el tiempo es capaz de producir un campo eléctrico. Por tanto, hay dos fuentes de campo eléctrico: las cargas eléctricas y un campo magnético variable en el tiempo.
1.4 Ley de Ampère
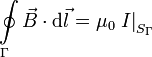
Aquí, Γ representa una línea cerrada y 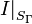 es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
es la corriente eléctrica que atraviesa una superficie cualquiera apoyada en la línea Γ.
Esta ley nos dice que
- Las corrientes eléctricas generan campos magnéticos.
- Las líneas de campo magnético generado por estas corrientes dan vueltas alrededor de las corrientes.
- El campo magnético se puede calcular a partir de la distribución de corriente eléctrica.





