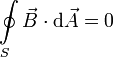Ecuaciones de Maxwell FII GIA
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Introducción == == Corriente de desplazamiento == == Ecuaciones de Maxwell == == Ondas electromagnéticas ==') |
(→Introducción) |
||
| Línea 1: | Línea 1: | ||
== Introducción == | == Introducción == | ||
| + | |||
| + | Los fenómenos electromagnéticos que hemos visto hasta ahora se pueden explicar con cuatro leyes básicas. Estas leyes, en su expresión integral, son | ||
| + | |||
| + | === Ley de Gauss === | ||
| + | |||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \oint\limits_S\vec{E}\cdot\mathrm{d}\vec{A} = \dfrac{Q_{\mathrm{int}}}{\varepsilon_0} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | === Ley de Gauss magnética === | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \oint\limits_S\vec{B}\cdot\mathrm{d}\vec{A} = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | === Ley de Faraday === | ||
| + | |||
| + | === Ley de Ampère === | ||
== Corriente de desplazamiento == | == Corriente de desplazamiento == | ||
Revisión de 13:59 29 abr 2011
Contenido |
1 Introducción
Los fenómenos electromagnéticos que hemos visto hasta ahora se pueden explicar con cuatro leyes básicas. Estas leyes, en su expresión integral, son
1.1 Ley de Gauss
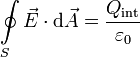
1.2 Ley de Gauss magnética